【题目】如图,在Rt△ABC中,∠B=90°,BC=5 ![]() ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)AC的长是 , AB的长是 .
(2)在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(4)当t为何值,△BEF的面积是2 ![]() ?
?
参考答案:
【答案】
(1)10;5
(2)
解:EF与AD平行且相等.
证明:在△DFC中,∠DFC=90°,∠C=30°,DC=2t,
∴DF=t.
又∵AE=t,
∴AE=DF,
∵AB⊥BC,DF⊥BC,
∴AE∥DF.
∴四边形AEFD为平行四边形.
∴EF与AD平行且相等
(3)
解:能;
理由如下:
∵AB⊥BC,DF⊥BC,
∴AE∥DF.
又∵AE=DF,
∴四边形AEFD为平行四边形.
∵AB=BCtan30°=5 ![]() ×
× ![]() =5,
=5,
∴AC=2AB=10.
∴AD=AC﹣DC=10﹣2t.
若使AEFD为菱形,则需AE=AD,
即t=10﹣2t,t= ![]() .
.
即当t= ![]() 时,四边形AEFD为菱形
时,四边形AEFD为菱形
(4)
解:∵在Rt△CDF中,∠A=30°,
∴DF= ![]() CD,
CD,
∴CF= ![]() t,
t,
又∵BE=AB﹣AE=5﹣t,BF=BC﹣CF=5 ![]() ﹣
﹣ ![]() t,
t,
∴ ![]() ,
,
即: ![]() ,
,
解得:t=3,t=7(不合题意舍去),
∴t=3.
故当t=3时,△BEF的面积为2 ![]() .
.
故答案为:5,10;平行且相等; ![]() ;3
;3
【解析】(1)解:∵在Rt△ABC中,∠C=30°,
∴AC=2AB,
根据勾股定理得:AC2﹣AB2=BC2 ,
∴3AB2=75,
∴AB=5,AC=10;
在Rt△ABC中,∠C=30°,则AC=2AB,根据勾股定理得到AC和AB的值.(2)先证四边形AEFD是平行四边形,从而证得AD∥EF,并且AD=EF,在运动过程中关系不变.(3)求得四边形AEFD为平行四边形,若使AEFD为菱形则需要满足的条件及求得.(4)BE=AB﹣AE=5﹣t,BF=BC﹣CF=5 ![]() ﹣
﹣ ![]() t,从而得到
t,从而得到 ![]() ,然后求得t的值.
,然后求得t的值.
【考点精析】掌握含30度角的直角三角形和勾股定理的概念是解答本题的根本,需要知道在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只方形水箱,其底面是边长为5米的正方形,箱内盛水,水深4米,现把一个棱长为3米的正方体沉入箱底,水面的高度将是( )
A.5.4米
B.7米
C.5.08米
D.6.67米 -
科目: 来源: 题型:
查看答案和解析>>【题目】小刘用84米长的铁丝围成一个长方形,要使长比宽多4米,则长方形的长为( )
A.29
B.27
C.25
D.23 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙二人在400米的环形跑道上练习同向竞走.乙每分钟走80米,甲每分钟走100米,现在甲在乙前100米,多少分钟后两人相遇?( )
A.5分钟
B.20分钟
C.15分钟
D.10分钟 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. x2x3=x5B. x6÷x2=x3C. x3+x3=x6D. 2x﹣x=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式:
 =
= 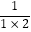 =1﹣
=1﹣  ,
,  =
= 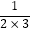 =
=  ﹣
﹣  ,
, 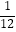 =
= 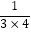 =
=  ﹣
﹣  ,
, 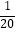 =
= 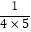 =
=  ﹣
﹣ 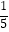 ,…
,…
(1)由此可推导出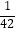 =;
=;
(2)猜想出能表示上述特点的一般规律,用含字母n的等式表示出来(n是正整数);
(3)请用(2)中的规律计算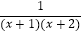 +
+ 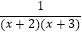 +…+
+…+ 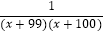 的结果.
的结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣a2)3+(﹣a3)2﹣a2a3;
(2)(3+a)(3﹣a)+a2;
(3)(x+y﹣3)(x+y+3);
(4)( )﹣2+(﹣2)3+|﹣3|﹣(π﹣3.14)0 .
)﹣2+(﹣2)3+|﹣3|﹣(π﹣3.14)0 .
相关试题

