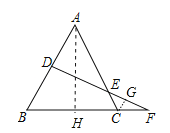
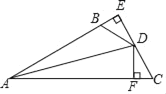
【题目】如图,已知△ABC中,AB=AC=![]() ,BC=4.线段AB的垂直平分线DF分别交边AB、AC、BC所在的直线于点D、E、F.
,BC=4.线段AB的垂直平分线DF分别交边AB、AC、BC所在的直线于点D、E、F.
(1)求线段BF的长;
(2)求AE:EC的值.

参考答案:
【答案】(1)![]() ;(2)5.
;(2)5.
【解析】分析:(1)作AH⊥BC于H,如图,利用等腰三角形的性质得BH=CH=![]() BC=2,再利用勾股定理计算出AH=4,然后证明Rt△FBD∽Rt△ABH,再利用相似比计算BF和DF的长;
BC=2,再利用勾股定理计算出AH=4,然后证明Rt△FBD∽Rt△ABH,再利用相似比计算BF和DF的长;
(2)作CG∥AB交DF于G,如图,利用CG∥BD得到![]() =
=![]() =
=![]() ,然后由CG∥AD,根据平行线分线段成比例定理得到AE:EC的值.
,然后由CG∥AD,根据平行线分线段成比例定理得到AE:EC的值.
详解:(1)作AH⊥BC于H,如图,
∵AB=AC=![]() ,∴BH=CH=
,∴BH=CH=![]() BC=2.
BC=2.
在Rt△ABH中,AH=![]() =4.
=4.
∵DF垂直平分AB,∴BD=![]() ,∠BDF=90°.
,∠BDF=90°.
∵∠ABH=∠FBD,∴Rt△FBD∽Rt△ABH,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∴BF=5,DF=2![]() ;
;
(2)作CG∥AB交DF于G,如图,
∵BF=5,BC=4,∴CF=1.
∵CG∥BD,∴![]() =
=![]() =
=![]() .
.
∵CG∥AD,∴![]() =
=![]() =
=![]() =5.
=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.
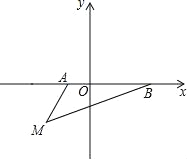
(1)填空:a= ,b= ;
(2)如果在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=
 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
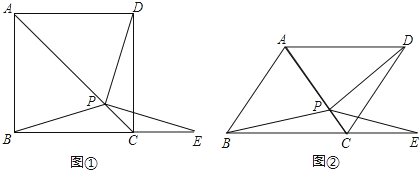
(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE= 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【阅读理解】
若
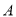 ,
, 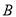 ,
,  为数轴上三点,若点
为数轴上三点,若点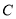 到
到 的距离是点
的距离是点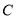 到
到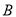 的距离的
的距离的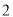 倍,我们就称点
倍,我们就称点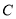 是
是 的优点.例如,如图①,点
的优点.例如,如图①,点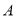 表示的数为
表示的数为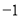 ,点
,点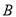 表示的数为
表示的数为 .表示数
.表示数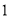 的点
的点 到点
到点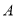 的距离是
的距离是 ,到点
,到点 的距离是
的距离是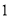 ,那么点
,那么点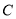 是
是 的优点;又如,表示
的优点;又如,表示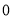 的点
的点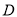 到点
到点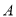 的距离是
的距离是 ,到点
,到点 的距离是
的距离是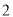 ,那么但点
,那么但点 是
是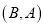 的好点.
的好点.【知识运用】
如图②,
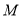 、
、 为数轴上两点,点
为数轴上两点,点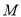 所表示的数为
所表示的数为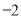 ,点
,点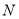 所表示的数为
所表示的数为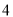 .
.(
 )数__________所表示的点是
)数__________所表示的点是 的优点.
的优点.(
 )如图③,
)如图③, ,
, 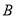 为数轴上两点,点
为数轴上两点,点 所表示的数为
所表示的数为 ,点
,点 所表示的数为
所表示的数为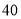 .现有一只电子蚂蚁
.现有一只电子蚂蚁 从点
从点 出发,以
出发,以 个单位每秒的速度向左运动,到达点
个单位每秒的速度向左运动,到达点 停止.当
停止.当 为何值时,
为何值时, 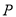 、
、 和
和 中恰有一个点为其余两点的好点?(请直接写出答案)
中恰有一个点为其余两点的好点?(请直接写出答案)

-
科目: 来源: 题型:
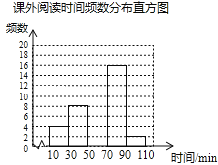
查看答案和解析>>【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如下不完整的统计表.
课外阅读时间t
频数
百分比
10≤t<30
4
8%
30≤t<50
8
16%
50≤t<70
a
40%
70≤t<90
16
b
90≤t<110
2
4%
合计
50
100%
请根据图表中提供的信息回答下列问题:
(1)a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若全校有900名学生,估计该校有多少学生平均每天的课外阅读时间不少于50min?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=
 cm,且tan∠EFC=
cm,且tan∠EFC= ,那么该矩形的周长为________.
,那么该矩形的周长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD平分∠EAC,DE⊥AB于E,DF⊥AC于F,BD=CD,
(1)求证:BE=FC;
(2)已知AC=20,BE=4,求AB的长.
相关试题

