【题目】如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
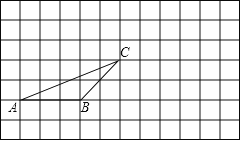
(1)画出△ABC中BC边上的高AD;
(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;
(3)若格点△PAB与格点△PBC的面积相等,则这样的点P共______个.
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)4
【解析】
(1)根据网格特点和正方形的性质画出高AD即可;
(2)利用网格特点和平移的性质画出△A1B1C1即可;
(3)建立直角坐标系,根据点到直线的距离公式列出方程求解即可得到两条直线,找出这两条直线上的格点即可.
(1)如图所示,AD即为所求;
(2)如图所示,△A1B1C1即为所求.
(3)如图,以B为原点,AB所在直线为x轴,过B点与AB垂直的直线为y轴,建立直角坐标系,设![]()
∴![]()
∴![]()
∴直线AB的解析式为y=0,直线BC的解析式为y=x
∵格点△PAB与格点△PBC的面积相等
∴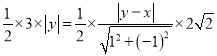
∴![]()
∴![]()
∴![]()
∴![]()
如图,作直线![]() 和直线
和直线![]() ,找出这两条直线上的格点即可
,找出这两条直线上的格点即可
这样的点P有4个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线,OC是∠AOD的平分线。
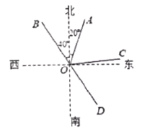
(1)求∠DOC的度数;
(2)求出射线OC的方向。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1=80°,∠2=100°,∠C=∠D.
(1)判断AC与DF的位置关系,并说明理由;
(2)若∠C比∠A大20°,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲同学在拼图探索活动中发现,用4个形状大小完全相同的直角三角形(直角边长分别为a,b,斜边长为c),可以拼成像如图1那样的正方形,并由此得出了关于a2,b2,c2的一个等式.
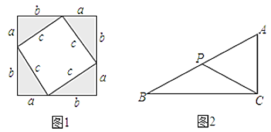
(1)请你写出这一结论:______,并给出验证过程.
(2)试用上述结论解决问题:如图2,P是Rt△ABC斜边AB上的一个动点,已知AC=5,AB=13,求PC的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB的函数解析式为y=-2x+8,与x轴交于点A,与y轴交于点B。
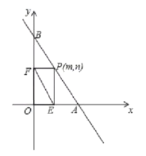
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接E,若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程ax2+bx﹣1=0(a≠0)有一根为x=2019,则一元二次方程a(x﹣1)2+b(x﹣1)=1必有一根为( )
A.
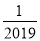 B.2020C.2019D.2018
B.2020C.2019D.2018
相关试题

