【题目】关于x的一元二次方程![]()
(1)求证:方程总有两个不相等的实数根。
(2)m为何整数时,此方程的两个根都是正整数?
(3)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求m的值。
参考答案:
【答案】(1)答案见解析;(2)m=2或者m=3;(3)m=![]()
【解析】
(1)计算根的判别式![]() ,证明
,证明![]() ;
;
(2)求出原方程的两个根,根据m为整数、两个不相等的正整数根得到m的值;
(3)分情况讨论:当AB=BC,或AC=BC时,5是一元二次方程的根,代入即可求出m的值,当AB=AC时AB、AC的长是这个方程的两个是实数根,由(1)可知方程有两个不相等的实数根,故此种情况不存在.
解:(1)∵![]()
∴![]()
=![]()
=4>0
∴方程总有两个不相等的实数根
(2)∵![]()
∴![]()
∴![]() ,
,![]()
∵方程的两个根都是正整数,且方程有两个不相等的实数根
∴![]() 是正整数,且
是正整数,且![]()
∴m=2或者m=3
(3)∵△ABC是等腰三角形,BC的长为5
∴当AB=BC,或AC=BC时,5是一元二次方程的根
即![]()
∴m=![]()
当AB=AC时
∵AB、AC的长是这个方程的两个是实数根
由(1)可知方程有两个不相等的实数根
∴此种情况不存在
∴m=![]()
-
科目: 来源: 题型:
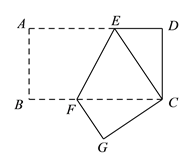
查看答案和解析>>【题目】已知将一矩形纸片ABCD折叠,使顶点A与C重合,折痕为EF.
(1)求证:CE=CF;
(2)若AB =8 cm,BC=16 cm,连接AF,写出求四边形AFCE面积的思路.
-
科目: 来源: 题型:
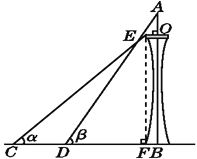
查看答案和解析>>【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)
-
科目: 来源: 题型:
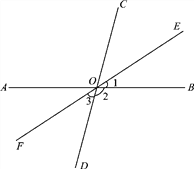
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,∠BOC=80°,OE是∠BOC的角平分线,OF是OE的反向延长线.
(1)求∠2、∠3的度数;
(2)说明OF平分∠AOD的理由.
-
科目: 来源: 题型:
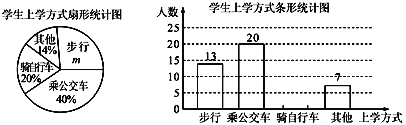
查看答案和解析>>【题目】某市决定在全市中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动,幸福中学为了了解学生的上学方式,在本校范围内随机抽查了部分学生,将收集的数据绘制成如下两副不完整的统计图(如图所示),请根据图中提供的信息,解答下列问题.
(1)m= %,这次共抽取 名学生进行调查;
(2)求骑自行车上学的人数?并补全条形图;
(3)在这次抽样调查中,采用哪种上学方式的人数最多?
(4)在扇形统计图中,步行所对应的扇形的圆心角的度数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某儿童游乐场为了有稳定的客源,决定开办会员业务,每张会员证30元,只限本人使用,有效期为一年,凭证入场每人次收费2元,不凭证入场每人次收费3元.
(1)一年内在这个游乐场玩多少次,办理会员证和不办理会员证花钱一样多?
(2)2019年,小明计划每月到游乐场玩4次,请你为他推荐一种经济省钱的方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
相关试题

