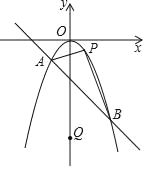
【题目】如图所示,已知抛物线y=ax2(a≠0)与一次函数y=kx+b的图象相交于A(﹣1,﹣1),B(2,﹣4)两点,点P是抛物线上不与A,B重合的一个动点,点Q是y轴上的一个动点.
(1)请直接写出a,k,b的值及关于x的不等式ax2<kx﹣2的解集;
(2)当点P在直线AB上方时,请求出△PAB面积的最大值并求出此时点P的坐标;
(3)是否存在以P,Q,A,B为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)a=﹣1,k=﹣1,b=﹣2,x<﹣1或x>2;(2)△PAB面积的最大值为![]() ,此时点P的坐标为(
,此时点P的坐标为(![]() ,
,![]() );(3)P的坐标为(﹣3,﹣9)或(3,﹣9)或(1,﹣1),Q的坐标为:Q(0,﹣12)或(0,﹣6)或(0,﹣4).
);(3)P的坐标为(﹣3,﹣9)或(3,﹣9)或(1,﹣1),Q的坐标为:Q(0,﹣12)或(0,﹣6)或(0,﹣4).
【解析】
(1)利用待定系数法即可求得a,k,b的值,根据图象即可得出不等式的解集;(2)过点A作y轴的平行线,过点B作x轴的平行线,两者交于点C,连接PC.设点P的横坐标为m,则点P的纵坐标为﹣m2.过点P作PD⊥AC于D,作PE⊥BC于E.则D(﹣1,﹣m2),E(m,﹣4),由此可得PD=m+1,PE=﹣m2+4.再根据S△APB=S△APC+S△BPC﹣S△ABC,代入数据即可得S△APB与m的二次函数关系式,利用二次函数求最值的方法求得m的值及S△APB 的值最大.再求得点P的坐标即可;(3)(3)根据平行四边形的性质和坐标特点解答即可.
解:(1)把A(﹣1,﹣1),代入y=ax2中,可得:a=﹣1,
把A(﹣1,﹣1),B(2,﹣4)代入y=kx+b中,可得:![]() ,
,
解得:![]() ,
,
所以a=﹣1,k=﹣1,b=﹣2,
关于x的不等式ax2<kx﹣2的解集是x<﹣1或x>2,
(2)过点A作y轴的平行线,过点B作x轴的平行线,两者交于点C.
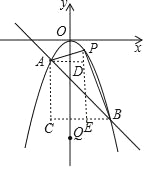
∵A(﹣1,﹣1),B(2,﹣4),
∴C(﹣1,﹣4),AC=BC=3,
设点P的横坐标为m,则点P的纵坐标为﹣m2.
过点P作PD⊥AC于D,作PE⊥BC于E.则D(﹣1,﹣m2),E(m,﹣4),
∴PD=m+1,PE=﹣m2+4.
∴S△APB=S△APC+S△BPC﹣S△ABC
=![]()
=![]()
=![]() .
.
∵![]() <0,
<0,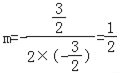 ,﹣1<m<2,
,﹣1<m<2,
∴当![]() 时,S△APB 的值最大.
时,S△APB 的值最大.
∴当![]() 时,
时,![]() ,S△APB=
,S△APB=![]() ,
,
即△PAB面积的最大值为![]() ,此时点P的坐标为(
,此时点P的坐标为(![]() ,
,![]() )
)
(3)存在三组符合条件的点,
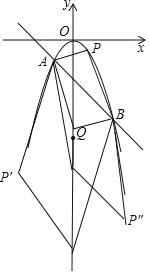
当以P,Q,A,B为顶点的四边形是平行四边形时,
∵AP=BQ,AQ=BP,A(﹣1,﹣1),B(2,﹣4),
可得坐标如下:
①P′的横坐标为﹣3,代入二次函数表达式,
解得:P'(﹣3,﹣9),Q'(0,﹣12);
②P″的横坐标为3,代入二次函数表达式,
解得:P″(3,﹣9),Q″(0,﹣6);
③P的横坐标为1,代入二次函数表达式,
解得:P(1,﹣1),Q(0,﹣4).
故:P的坐标为(﹣3,﹣9)或(3,﹣9)或(1,﹣1),
Q的坐标为:Q(0,﹣12)或(0,﹣6)或(0,﹣4).
-
科目: 来源: 题型:
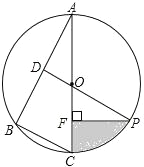
查看答案和解析>>【题目】如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=4,点D是AB的中点,连接DO并延长交⊙O于点P.
(1)求劣弧PC的长(结果保留π);
(2)过点P作PF⊥AC于点F,求阴影部分的面积(结果保留π).
-
科目: 来源: 题型:
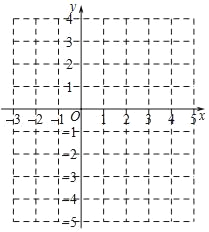
查看答案和解析>>【题目】二次函数y=ax2﹣2ax﹣3(a≠0)的图象经过点A.
(1)求二次函数的对称轴;
(2)当A(﹣1,0)时,
①求此时二次函数的表达式;
②把y=ax2﹣2ax﹣3化为y=a(x﹣h)2+k的形式,并写出顶点坐标;
③画出函数的图象.
-
科目: 来源: 题型:
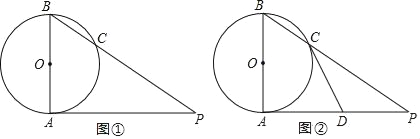
查看答案和解析>>【题目】已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若∠P=35°,连OC,求∠BOC的度数;
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
-
科目: 来源: 题型:
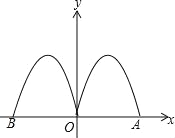
查看答案和解析>>【题目】如图,抛物线y=﹣2x2+4x与x轴交于点O、A,把抛物线在x轴及其上方的部分记为C1,将C1以y铀为对称轴作轴对称得到C2,C2与x轴交于点B,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是( )
A. 0<m<
 B.
B.  <m<
<m<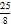
C. 0<m<
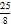 D. m<
D. m< 或m<
或m<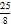
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示双曲线y=
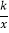 与y=﹣
与y=﹣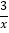 分别位于第三象限和第二象限,A是y轴上任意一点,B是y=﹣
分别位于第三象限和第二象限,A是y轴上任意一点,B是y=﹣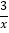 上的点,C是y=
上的点,C是y=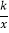 上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=
上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=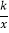 在每个象限内,y随x的增大而减小;②若点B的横坐标为﹣3,则C点的坐标为(﹣3,
在每个象限内,y随x的增大而减小;②若点B的横坐标为﹣3,则C点的坐标为(﹣3, );③k=4;④△ABC的面积为定值7,正确的有( )
);③k=4;④△ABC的面积为定值7,正确的有( )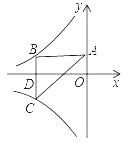
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过x min时,A、B两组材料的温度分别为yA℃、yB℃,yA、yB与x的函数关系式分别为yA=kx+b,yB=
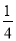 (x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
(x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
(1)分别求yA、yB关于x的函数关系式;
(2)当A组材料的温度降至120℃时,B组材料的温度是多少?
(3)在0<x<40的什么时刻,两组材料温差最大?
相关试题

