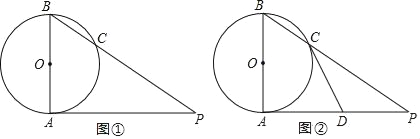
【题目】已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若∠P=35°,连OC,求∠BOC的度数;
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
参考答案:
【答案】(1)∠BOC=70°;(2)详见解析.
【解析】
(1)连接OC.已知AP是⊙O的切线,根据切线的性质可得∠PAB=90°,再由直角三角形的两锐角互余求出∠B=55°,最后利用等腰三角形的性质及三角形的内角和定理即可解决问题;(2)如图②中,连接OC,OD,AC.根据已知条件易证△ODC≌△ODA,由全等三角形的性质可得∠OCD=∠OAD=90°,由此即可证得结论.
解:(1)如图①中,连接OC.
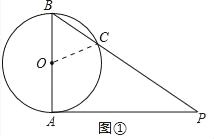
∵PA是⊙O的切线,
∴PA⊥AB,
∴∠PAB=90°,
∵∠P=35°,
∴∠B=55°,
∵OB=OC,
∴∠B=∠OCB=55°,
∴∠BOC=180°﹣55°﹣55°=70°.
(2)如图②中,连接OC,OD,AC.
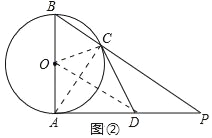
∵AB是直径,
∴∠ACB=∠ACP=90°,
∵AD=DP,
∴DC=DA=DB,
∵OA=OC,OD=OD,
∴△ODC≌△ODA(SSS),
∴∠OCD=∠OAD=90°,
∴OC⊥CD,
∴DC是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】济南某中学在参加“创文明城,点赞泉城”书画比赛中,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作鼎的数量进行了分析统计,制作了两幅不完整的统计图.

请根据以上信息,回答下列问题:
(l)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请补充完整条形统计图,并计算扇形统计图中C班作品数量所对应的圆心角度数 .
(3)请估计全校共征集作品的什数.
(4)如果全枝征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一样等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
-
科目: 来源: 题型:
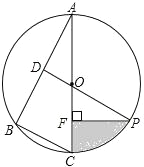
查看答案和解析>>【题目】如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=4,点D是AB的中点,连接DO并延长交⊙O于点P.
(1)求劣弧PC的长(结果保留π);
(2)过点P作PF⊥AC于点F,求阴影部分的面积(结果保留π).
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2﹣2ax﹣3(a≠0)的图象经过点A.
(1)求二次函数的对称轴;
(2)当A(﹣1,0)时,
①求此时二次函数的表达式;
②把y=ax2﹣2ax﹣3化为y=a(x﹣h)2+k的形式,并写出顶点坐标;
③画出函数的图象.
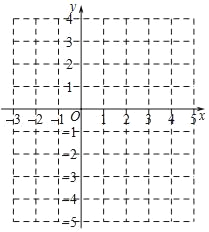
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知抛物线y=ax2(a≠0)与一次函数y=kx+b的图象相交于A(﹣1,﹣1),B(2,﹣4)两点,点P是抛物线上不与A,B重合的一个动点,点Q是y轴上的一个动点.
(1)请直接写出a,k,b的值及关于x的不等式ax2<kx﹣2的解集;
(2)当点P在直线AB上方时,请求出△PAB面积的最大值并求出此时点P的坐标;
(3)是否存在以P,Q,A,B为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.
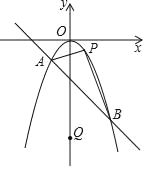
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣2x2+4x与x轴交于点O、A,把抛物线在x轴及其上方的部分记为C1,将C1以y铀为对称轴作轴对称得到C2,C2与x轴交于点B,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是( )
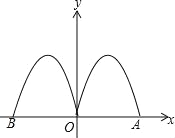
A. 0<m<
 B.
B.  <m<
<m<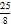
C. 0<m<
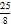 D. m<
D. m< 或m<
或m<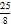
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示双曲线y=
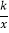 与y=﹣
与y=﹣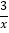 分别位于第三象限和第二象限,A是y轴上任意一点,B是y=﹣
分别位于第三象限和第二象限,A是y轴上任意一点,B是y=﹣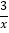 上的点,C是y=
上的点,C是y=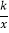 上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=
上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=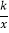 在每个象限内,y随x的增大而减小;②若点B的横坐标为﹣3,则C点的坐标为(﹣3,
在每个象限内,y随x的增大而减小;②若点B的横坐标为﹣3,则C点的坐标为(﹣3, );③k=4;④△ABC的面积为定值7,正确的有( )
);③k=4;④△ABC的面积为定值7,正确的有( )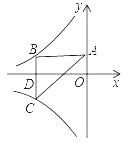
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

