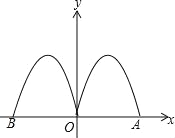
【题目】如图,抛物线y=﹣2x2+4x与x轴交于点O、A,把抛物线在x轴及其上方的部分记为C1,将C1以y铀为对称轴作轴对称得到C2,C2与x轴交于点B,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是( )
A. 0<m<![]() B.
B. ![]() <m<
<m<![]()
C. 0<m<![]() D. m<
D. m<![]() 或m<
或m<![]()
参考答案:
【答案】A
【解析】
首先求出点A和点B的坐标,然后求出C2解析式,分别求出直线y=x+m与抛物线C1相切时m的值以及直线y=x+m过原点时m的值,结合图形即可得到答案.
令![]()
解得:x=0或x=2,
则点A(2,0),B(2,0),
∵C1与C2关于y铀对称,C1:![]()
∴C2解析式为![]()
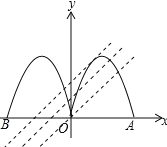
当y=x+m与C1相切时,如图所示:
令![]()
即![]()
![]()
解得![]()
当y=x+m过原点时,m=0,
∴当![]() 时直线y=x+m与C1、C2共有3个不同的交点,
时直线y=x+m与C1、C2共有3个不同的交点,
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
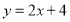 的图象与
的图象与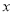 轴、
轴、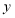 轴分别交于
轴分别交于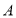 、
、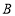 两点,
两点,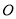 是坐标原点.
是坐标原点.(1)求交点
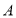 、
、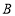 的坐标,并画出该一次函数的图象;
的坐标,并画出该一次函数的图象;(2)求
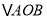 的面积;
的面积;(3)根据图象直接写出:当
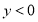 时,
时,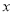 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】端午节期间,某食品店平均每天可卖出300只粽子,卖出1只粽子的利润是1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获取的利润更多,该店决定把零售单价下降m(0<m<1)元.
(1)零售单价下降m元后,该店平均每天可卖出_____只粽子,利润为_____元.
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元并且卖出的粽子更多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数 y=
 x﹣3 与反比例函数 y=
x﹣3 与反比例函数 y= 的图象相交于点 A(4,n),与 x 轴相交于点 B.
的图象相交于点 A(4,n),与 x 轴相交于点 B.(1)求 n 与 k 的值;
(2)以 AB 为边作菱形 ABCD,使点 C 在 x 轴正半轴上,点 D 在第一象限,求点 D 的坐标;
(3)观察反比例函数y=
 的图象,当 y>﹣2 时,请直接写出自变量 x 的取值范围.
的图象,当 y>﹣2 时,请直接写出自变量 x 的取值范围.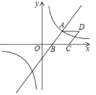
-
科目: 来源: 题型:
查看答案和解析>>【题目】为支援灾区,某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同.
(1)求A、B两种学习用品的单价各是多少元?
(2)若购买这批学习用品的费用不超过28000元,则最多购买B型学习用品多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售一种水果,迸价为每箱40元,规定售价不低于进价.现在的售价为每箱72元,每月可销售60箱.经市场调查发现:若这种牛奶的售价每降低2元,则每月的销量将增加10箱,设每箱水果降价x元(x为偶数),每月的销量为y箱.
(1)写出y与x之间的函数关系式和自变量x的取值范围.
(2)若该超市在销售过程中每月需支出其他费用500元,则如何定价才能使每月销售水果的利润最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公园要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水.连喷头在内,柱高0.8m.水流在各个方向上沿形状相同的抛物线路径落下,如图(1)所示.
根据设计图纸已知:如图(2)中所示直角坐标系中,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是 y=﹣x2+2x+
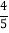 .
.(1)喷出的水流距水平面的最大高度是多少?
(2)如果不计其他因素,那么水池半径至少为多少时,才能使喷出的水流都落在水池内?
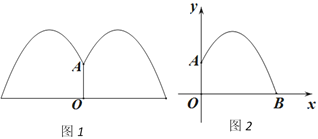
相关试题

