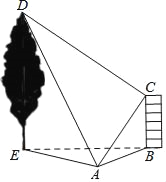
【题目】如图,在水平地面上有一幢房屋BC与一棵树DE,在地面观测点A处测得屋顶C与树梢D的仰角分别是45°与60°,∠CAD=60°,在屋顶C处测得∠DCA=90°.若房屋的高BC=6米,则树高DE的长度为( )
A. 3![]() B. 6
B. 6![]() C. 3
C. 3![]() D. 6
D. 6![]()
参考答案:
【答案】D
【解析】分析:首先解Rt△ABC,求出AC,再解Rt△ACD,求出AD,再解Rt△DEA,即可得到DE的长.
详解:如图,
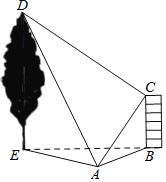
∵在Rt△ABC中,∠ABC=90°,∠CAB=45°,BC=6m,
∴AC=![]() BC=6
BC=6![]() m;
m;
∵在Rt△ACD中,∠DCA=90°,∠CAD=60°,
∴∠ADC=30°,
∴AD=2AC=12![]() 米;
米;
∵在Rt△DEA中,∠AED=90°,∠EAD=60°,
∴DE=ADsin60°=6![]() 米,
米,
答:树高DE的长度为6![]() 米.
米.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,点
 为直线
为直线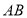 上一点,过点
上一点,过点 作射线
作射线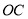 ,将一直角三角板如图摆放(
,将一直角三角板如图摆放(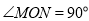 ).
).(1)若
 ,求
,求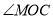 的大小.
的大小.(2)将图①中的三角板绕点
 旋转一定的角度得图②,使边
旋转一定的角度得图②,使边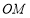 恰好平分
恰好平分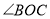 ,问:
,问: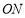 是否平分
是否平分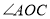 ?请说明理由.
?请说明理由.(3)将图①中的三角板绕点
 旋转一定的角度得图③,使边
旋转一定的角度得图③,使边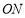 在
在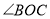 的内部,如果
的内部,如果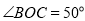 ,则
,则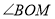 与
与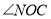 之间存在怎样的数量关系?请说明理由.
之间存在怎样的数量关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,适宜采用全面调查(普查)方式的是( )
A.了解我国民众对乐天集团“萨德事件”的看法
B.调查我校某班学生喜欢上数学课的情况
C.了解湖南卫视《人们的名义》反腐剧的收视率
D.调查某类烟花爆竹燃放的安全情况
-
科目: 来源: 题型:
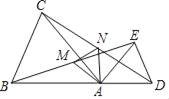
查看答案和解析>>【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在同一条直线上,M,N分别为BE,CD的中点.
(1)求证:△ABE≌ACD;
(2)判断△AMN的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )

A. 第24天的销售量为200件 B. 第10天销售一件产品的利润是15元
C. 第12天与第30天这两天的日销售利润相等 D. 第30天的日销售利润是750元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则sin∠BED的值是( )

A.
 B.
B.  C.
C.  D.
D. 
相关试题

