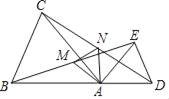
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在同一条直线上,M,N分别为BE,CD的中点.
(1)求证:△ABE≌ACD;
(2)判断△AMN的形状,并说明理由.
参考答案:
【答案】(1)证明见解析(2)△AMN为等腰三角形;理由见解析
【解析】
(1)由∠BAC=∠DAE,等式左右两边都加上∠CAE,得到一对角相等,再由AB=AC,AD=AE,利用SAS可得出三角形ABE与三角形ACD全等;
(2)由M与N分别为BE,CD的中点,且BE=CD,可得出ME=ND,由△ABE与△ACD全等,对应角∠AEB=∠ADC,利用SAS可得出△AME与△AND全等,利用全等三角形的对应边相等可得出AM=AN,即△AMN为等腰三角形.
(1)∵∠BAC=∠DAE,
∴∠BAC+∠CAE=∠DAE+∠CAE,即∠BAE=∠CAD,
在△ABE和△ACD中,
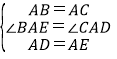 ,
,
∴△ABE≌△ACD(SAS);
(2)∵△ABE≌△ACD
∴BE=CD,∠AEM=∠ADC,
∵M、N分别为BE、CD的中点,
∴ME=ND,
在△AEM和△ADN中,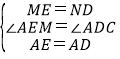 ,
,
∴△AEM≌△ADN(SAS),
∴AM=AN,
即△AMN为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点A为半圆O直径MN所在直线上一点,射线AB垂直于MN,垂足为A,半圆绕M点顺时针转动,转过的角度记作a;设半圆O的半径为R,AM的长度为m,回答下列问题:

探究:
(1)若R=2,m=1,如图1,当旋转30°时,圆心O′到射线AB的距离是;如图2,当a=°时,半圆O与射线AB相切;
(2)如图3,在(1)的条件下,为了使得半圆O转动30°即能与射线AB相切,在保持线段AM长度不变的条件下,调整半径R的大小,请你求出满足要求的R,并说明理由.
(3)发现:如图4,在0°<α<90°时,为了对任意旋转角都保证半圆O与射线AB能够相切,小明探究了cosα与R、m两个量的关系,请你帮助他直接写出这个关系;cosα=(用含有R、m的代数式表示)
(4)拓展:如图5,若R=m,当半圆弧线与射线AB有两个交点时,α的取值范围是 , 并求出在这个变化过程中阴影部分(弓形)面积的最大值(用m表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】a是不为1的有理数,我们把
 称为a的差倒数.如:2的差倒数是
称为a的差倒数.如:2的差倒数是 ,现已知a1=
,现已知a1= ,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…
,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,… (1)求a2,a3,a4的值;
(2)根据(1)的计算结果,请猜想并写出a2016a2017a2018的值;
(3)计算:a33+a66+a99+…+a9999的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:
①∠ABC=∠ADC;
②AC与BD相互平分;
③AC,BD分别平分四边形ABCD的两组对角;
④四边形ABCD的面积S=
 ACBD.
ACBD.正确的是 (填写所有正确结论的序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),直接写出线段AD与NE的数量关系为 .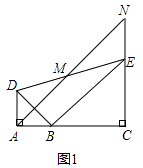
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),判断△ACN是什么特殊三角形并说明理由.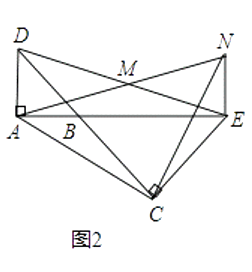
(3)将图1中△BCE绕点B旋转到图3位置,此时A,B,M三点在同一直线上.若AC=3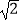 ,AD=1,则四边形ACEN的面积为 .
,AD=1,则四边形ACEN的面积为 . 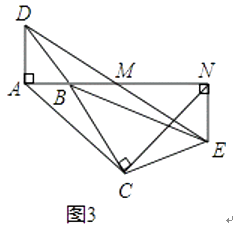
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,CE交AB于点F,若∠E=20°,∠C=45°,则∠A的度数为( )

A. 5° B. 15° C. 25° D. 35°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.
(1)正方形ABCD的面积为 ,边长为 ,对角线BD= ;
(2)求证:
 ;
;(3)如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 ,若点E所表示的数为整数,则点E所表示的数为 .


相关试题

