【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒2个单位长度的速度向点
方向以每秒2个单位长度的速度向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒1个单位长度的速度向点
方向以每秒1个单位长度的速度向点![]() 运动,当其中一个点到达终点时,另一个点也随之停止运动,设点
运动,当其中一个点到达终点时,另一个点也随之停止运动,设点![]() ,
,![]() 运动的时间是
运动的时间是![]() 秒(
秒(![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.

(1)求![]() 、
、![]() 的长;
的长;
(2)求证:![]() ;
;
(3)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,说明理由.
值;如果不能,说明理由.
参考答案:
【答案】(1)![]() ;(2)见解析;(3)四边形
;(2)见解析;(3)四边形![]() 能够成为菱形,
能够成为菱形,![]() .
.
【解析】
(1)根据![]() 可知
可知![]() ,然后再利用勾股定理
,然后再利用勾股定理![]() 即可求出AB,AC的长度;
即可求出AB,AC的长度;
(2)分别用含t的代数式表示出AE,DF,即可证明![]() ;
;
(3)首先可以证明四边形![]() 是平行四边形,要使平行四边形
是平行四边形,要使平行四边形![]() 是菱形,只要
是菱形,只要![]() 即可,由此可建立一个关于t的方程,解方程即可得出答案.
即可,由此可建立一个关于t的方程,解方程即可得出答案.
(1)∵![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ;
;
(2)证明:∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ;
;
(3)四边形![]() 能够成为菱形,
能够成为菱形,
∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴四边形![]() 是平行四边形.
是平行四边形.
要使平行四边形![]() 是菱形,只要
是菱形,只要![]() 即可,
即可,
即![]() ,
,
解得![]() ,
,
∴当![]() 时,四边形
时,四边形![]() 为菱形.
为菱形.
-
科目: 来源: 题型:
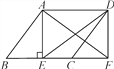
查看答案和解析>>【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A(0,m+4),点C(5m+3,0)在x轴的正半轴上,现将点C向左平移4单位长度再向上平移7个单位长度得到对应点B(7m﹣7,n).
(1)求m,n的值;
(2)若点P从点C出发以每秒2个单位长度/秒的速度沿CO方向移动,同时点Q从点O出发以每秒1个单位长度的速度沿OA方向移动,设移动的时间为t秒(0<t<7),四边形OPBA与△OQB的面积分别记为S1,S2.是否存在一段时间,使S1<2S2?若存在,求出t的取值范围;若不存在,试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,在平面直角坐标系中,点
,在平面直角坐标系中,点 ,
, 的坐标分别为
的坐标分别为 ,
, ,将线段
,将线段 先向上平移
先向上平移 个单位长度,再向右平移
个单位长度,再向右平移 个单位长度,得到线段
个单位长度,得到线段 ,连接
,连接 ,
, ,构成平行四边形
,构成平行四边形 .
. (1)请写出点
 的坐标为________,点
的坐标为________,点 的坐标为________,
的坐标为________, ________;
________;(2)点
 在
在 轴上,且
轴上,且 ,求出点
,求出点 的坐标;
的坐标;(3)如图
 ,点
,点 是线段
是线段 上任意一个点(不与
上任意一个点(不与 、
、 重合),连接
重合),连接 、
、 ,试探索
,试探索 、
、 、
、 之间的关系,并证明你的结论.
之间的关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )

A.3
B.4
C.1
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 在直角坐标系中,
在直角坐标系中, 请写出
请写出 各点的坐标.
各点的坐标. 若把
若把 向上平移2个单位,再向左平移1个单位得到
向上平移2个单位,再向左平移1个单位得到 ,写出
,写出 、
、 、
、 的坐标,并在图中画出平移后图形.
的坐标,并在图中画出平移后图形. 求出三角形ABC的面积.
求出三角形ABC的面积.
相关试题

