【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )

A.3
B.4
C.1
D.2
参考答案:
【答案】A
【解析】
首先连接BD,易证得△ADE≌△BDF,然后可证得DE=DF,AE=BF,即可得△DEF是等边三角形,然后可证得∠ADE=∠BEF.
连接BD,
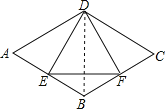
∵四边形ABCD是菱形,
∴AD=AB,∠ADB=![]() ∠ADC,AB∥CD,
∠ADC,AB∥CD,
∵∠A=60°,
∴∠ADC=120°,∠ADB=60°,
同理:∠DBF=60°,
即∠A=∠DBF,
∴△ABD是等边三角形,
∴AD=BD,
∵∠ADE+∠BDE=60°,∠BDE+∠BDF=∠EDF=60°,
∴∠ADE=∠BDF,
∵在△ADE和△BDF中,
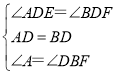 ,
,
∴△ADE≌△BDF(ASA),
∴DE=DF,AE=BF,故①正确;
∵∠EDF=60°,
∴△EDF是等边三角形,
∴②正确;
∴∠DEF=60°,
∴∠AED+∠BEF=120°,
∵∠AED+∠ADE=180°-∠A=120°,
∴∠ADE=∠BEF;
故④正确;
∵△ADE≌△BDF,
∴AE=BF,
同理:BE=CF,
但BE不一定等于BF,
故③错误.
综上所述,结论正确的是①②④.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,在平面直角坐标系中,点
,在平面直角坐标系中,点 ,
, 的坐标分别为
的坐标分别为 ,
, ,将线段
,将线段 先向上平移
先向上平移 个单位长度,再向右平移
个单位长度,再向右平移 个单位长度,得到线段
个单位长度,得到线段 ,连接
,连接 ,
, ,构成平行四边形
,构成平行四边形 .
. (1)请写出点
 的坐标为________,点
的坐标为________,点 的坐标为________,
的坐标为________, ________;
________;(2)点
 在
在 轴上,且
轴上,且 ,求出点
,求出点 的坐标;
的坐标;(3)如图
 ,点
,点 是线段
是线段 上任意一个点(不与
上任意一个点(不与 、
、 重合),连接
重合),连接 、
、 ,试探索
,试探索 、
、 、
、 之间的关系,并证明你的结论.
之间的关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
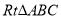 中,
中,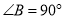 ,
, ,
, ,点
,点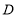 从点
从点 出发沿
出发沿 方向以每秒2个单位长度的速度向点
方向以每秒2个单位长度的速度向点 运动,同时点
运动,同时点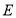 从点
从点 出发沿
出发沿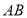 方向以每秒1个单位长度的速度向点
方向以每秒1个单位长度的速度向点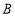 运动,当其中一个点到达终点时,另一个点也随之停止运动,设点
运动,当其中一个点到达终点时,另一个点也随之停止运动,设点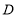 ,
,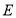 运动的时间是
运动的时间是 秒(
秒(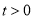 ).过点
).过点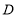 作
作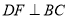 于点
于点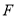 ,连接
,连接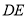 、
、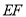 .
.
(1)求
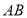 、
、 的长;
的长;(2)求证:
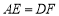 ;
;(3)四边形
 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的 值;如果不能,说明理由.
值;如果不能,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 在直角坐标系中,
在直角坐标系中, 请写出
请写出 各点的坐标.
各点的坐标. 若把
若把 向上平移2个单位,再向左平移1个单位得到
向上平移2个单位,再向左平移1个单位得到 ,写出
,写出 、
、 、
、 的坐标,并在图中画出平移后图形.
的坐标,并在图中画出平移后图形. 求出三角形ABC的面积.
求出三角形ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程变形正确的是( )
A.方程3x﹣2=2x﹣1移项,得3x﹣2x=﹣1﹣2
B.方程3﹣x=2﹣5(x﹣1)去括号,得3﹣x=2﹣5x﹣1
C.方程 可化为3x=6.
可化为3x=6.
D.方程 系数化为1,得x=﹣1
系数化为1,得x=﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中不正确的是( )
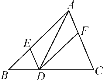
A.四边形AEDF是平行四边形
B.若∠BAC=90°,则四边形AEDF是矩形
C.若AD平分∠BAC,则四边形AEDF是矩形
D.若AD⊥BC且AB=AC,则四边形AEDF是菱形
相关试题

