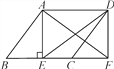
【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)先证明四边形AEFD是平行四边形,再证明∠AEF=90°即可.
(2)证明△ABF是直角三角形,由三角形的面积即可得出AE的长.
试题解析:(1)证明:∵CF=BE,
∴CF+EC=BE+EC.
即EF=BC.
∵在ABCD中,AD∥BC且AD=BC,
∴AD∥EF且AD=EF.
∴四边形AEFD是平行四边形.
∵AE⊥BC,
∴∠AEF=90°.
∴四边形AEFD是矩形;
(2)∵四边形AEFD是矩形,DE=8,
∴AF=DE=8.
∵AB=6,BF=10,
∴AB2+AF2=62+82=100=BF2.
∴∠BAF=90°.
∵AE⊥BF,
∴△ABF的面积=![]() ABAF=
ABAF=![]() BFAE.
BFAE.
∴AE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和对称轴.
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?
(3)若将点E移至图2的位置,此时∠B,∠D,∠E之间有什么关系?
(4)若将点E移至图3的位置,此时∠B,∠D,∠E之间的关系又如何?
(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A(0,m+4),点C(5m+3,0)在x轴的正半轴上,现将点C向左平移4单位长度再向上平移7个单位长度得到对应点B(7m﹣7,n).
(1)求m,n的值;
(2)若点P从点C出发以每秒2个单位长度/秒的速度沿CO方向移动,同时点Q从点O出发以每秒1个单位长度的速度沿OA方向移动,设移动的时间为t秒(0<t<7),四边形OPBA与△OQB的面积分别记为S1,S2.是否存在一段时间,使S1<2S2?若存在,求出t的取值范围;若不存在,试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,在平面直角坐标系中,点
,在平面直角坐标系中,点 ,
, 的坐标分别为
的坐标分别为 ,
, ,将线段
,将线段 先向上平移
先向上平移 个单位长度,再向右平移
个单位长度,再向右平移 个单位长度,得到线段
个单位长度,得到线段 ,连接
,连接 ,
, ,构成平行四边形
,构成平行四边形 .
. (1)请写出点
 的坐标为________,点
的坐标为________,点 的坐标为________,
的坐标为________, ________;
________;(2)点
 在
在 轴上,且
轴上,且 ,求出点
,求出点 的坐标;
的坐标;(3)如图
 ,点
,点 是线段
是线段 上任意一个点(不与
上任意一个点(不与 、
、 重合),连接
重合),连接 、
、 ,试探索
,试探索 、
、 、
、 之间的关系,并证明你的结论.
之间的关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
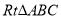 中,
中,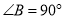 ,
, ,
, ,点
,点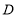 从点
从点 出发沿
出发沿 方向以每秒2个单位长度的速度向点
方向以每秒2个单位长度的速度向点 运动,同时点
运动,同时点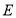 从点
从点 出发沿
出发沿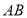 方向以每秒1个单位长度的速度向点
方向以每秒1个单位长度的速度向点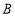 运动,当其中一个点到达终点时,另一个点也随之停止运动,设点
运动,当其中一个点到达终点时,另一个点也随之停止运动,设点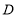 ,
,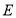 运动的时间是
运动的时间是 秒(
秒(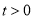 ).过点
).过点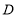 作
作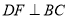 于点
于点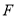 ,连接
,连接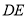 、
、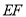 .
.
(1)求
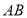 、
、 的长;
的长;(2)求证:
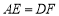 ;
;(3)四边形
 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的 值;如果不能,说明理由.
值;如果不能,说明理由.
相关试题

