【题目】如图,两个以点O为圆心的同心圆,
图1 图2
(1)如图1,大圆的弦AB交小圆于C,D两点,试判断AC与BD的数量关系,并说明理由.
(2)如图2,将大圆的弦AB向下平移使其为小圆的切线,切点为C,证明:AC=BC.
(3)在(2)的基础上,已知AB=20cm,直接写出圆环的面积.
参考答案:
【答案】
(1)解:AC=BD,理由是:
过O作OH⊥AB,由垂径定理得AH=BH,CH=DH,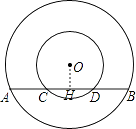
AH-CH=BH-DH,
即AC=BD
(2)解:连接OC,如图,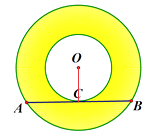
AB是小圆的切线,
OC⊥AB,则AC=BC
(3)解:如图,连接OB.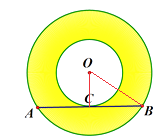
∵大圆的弦AB是小圆的切线, ∴OC⊥AB,AC=CB, ∴OB2-OC2=(20÷2)2=102 , ∵S圆环=S大-S小=πOB2-πOC2=π(OB2-OC2), ∴S圆环=100πcm2
【解析】(1)AC=BD,理由是:过O作OH⊥AB,由垂径定理得AH=BH,CH=DH,根据等式的性质得出AH-CH=BH-DH,从而得出AC=BD ;
(2)连接OC,如图,根据切线的性质定理得出OC⊥AB,再根据垂径定理得出AC=BC ;
(3)连接OB.根据切线的性质定理得出OC⊥AB,再根据垂径定理得出AC=BC ,然后根据勾股定理及等式的性质得出OB2-OC2=(20÷2)2=102 ,然后根据S圆环=S大-S小=πOB2-πOC2=π(OB2-OC2)算出答案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1所示,△ABC中,∠ACB的角平分线CF与∠EAC的角平分线AD的反向延长线交于点F;
①若∠B=90°则∠F= ;
②若∠B=a,求∠F的度数(用a表示);
(2)如图2所示,若点G是CB延长线上任意一动点,连接AG,∠AGB与∠GAB的角平分线交于点H,随着点G的运动,∠F+∠H的值是否变化?若变化,请说明理由;若不变,请求出其值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(十九),用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?

(A) 5 (B) 6 (C) 7 (D) 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数的图象与反比例函数的图象相交于A、B两点。

(1)利用图中的条件,求反比例函数和一次函数的解析式;
(2)根据图象直接写出一次函数的值大于反比例函数的x的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
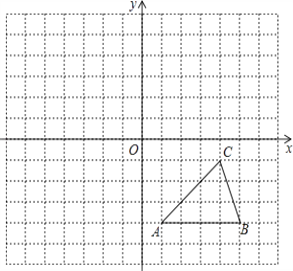
(1)写出A、B、C的坐标.
(2)以原点O为中心,将△ABC围绕原点O逆时针旋转180°得到△A1B1C1 , 画出△A1B1C1 .
(3)求(2)中C到C1经过的路径以及OB扫过的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于
 MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则S△DAC:S△ABC=_____.
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则S△DAC:S△ABC=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)
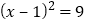
(2)

(3)

(4)

相关试题

