【题目】解方程
(1)![]()
(2)![]()
(3)![]()
(4)
参考答案:
【答案】(1)x1=4,x2=-2;(2)x=![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .
.
【解析】
(1)直接开平方即可;(2)两边同时除以8,开立方即可;(3)利用加减消元法先求出y的值,再代入求出x的值即可;(4)![]() 去分母得3x+2y=7,利用代入消元法求出x的值,进而求出y值即可.
去分母得3x+2y=7,利用代入消元法求出x的值,进而求出y值即可.
(1)![]()
x-1=±3
x1=4,x2=-2.
(2)![]()
(x+2)3=![]()
x+2=![]()
x=![]() .
.
(3)![]()
②-①得3y=-3,
解得:y=-1,
把y=-1代入①得x=2,
∴原方程组的解为![]() .
.
(4)
由②得3(x-1)+2(y+1)=6,
整理得:3x+2y=7③,
由①得:y=4-x,
把y=4-x代入③得:3x+8-2x=7,
解得:x=-1,
把x=-1代入①得y=5,
∴原方程组的解为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个以点O为圆心的同心圆,

图1 图2
(1)如图1,大圆的弦AB交小圆于C,D两点,试判断AC与BD的数量关系,并说明理由.
(2)如图2,将大圆的弦AB向下平移使其为小圆的切线,切点为C,证明:AC=BC.
(3)在(2)的基础上,已知AB=20cm,直接写出圆环的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
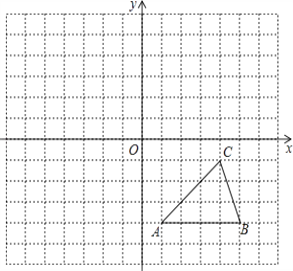
(1)写出A、B、C的坐标.
(2)以原点O为中心,将△ABC围绕原点O逆时针旋转180°得到△A1B1C1 , 画出△A1B1C1 .
(3)求(2)中C到C1经过的路径以及OB扫过的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于
 MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则S△DAC:S△ABC=_____.
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则S△DAC:S△ABC=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.

(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图

(1)分别写出下列各点的坐标:A′______;B′______;C′______
(2)若点P(m,n)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为______.
(3)求△ABC的面积.
相关试题

