【题目】如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 . 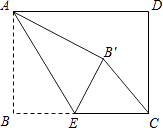
参考答案:
【答案】![]() 或3
或3![]()
【解析】解:当△CEB′为直角三角形时,有两种情况: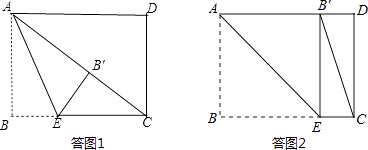
①当点B′落在矩形内部时,如答图1所示.
连结AC,
在Rt△ABC中,AB=3,BC=4,
∴AC= ![]() =5,
=5,
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
∴EB=EB′,AB=AB′=3,
∴CB′=5﹣3=2,
设BE=x,则EB′=x,CE=4﹣x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2 ,
∴x2+22=(4﹣x)2 , 解得x= ![]() ,
,
∴BE= ![]() ;
;
②当点B′落在AD边上时,如答图2所示.
此时ABEB′为正方形,∴BE=AB=3.
综上所述,BE的长为 ![]() 或3.
或3.
故答案为: ![]() 或3.
或3.
当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如答图1所示.连结AC,先利用勾股定理计算出AC=5,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=3,可计算出CB′=2,设BE=x,则EB′=x,CE=4﹣x,然后在Rt△CEB′中运用勾股定理可计算出x.②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决群众看病贵的问题,有关部门决定降低药价,原价为30元的药品经过连续两次降价,价格变为24.3元,则平均每次降价的百分率为( )
A.10%B.15%C.20%D.25%
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,举行抽奖活动,并规定:顾客每购买100元的商品,就可以随机抽取一张奖券,抽得奖券“紫气东来”、“化开富贵”、“吉星高照”,就可以分别获得100元、50元、20元的购物券,抽得“谢谢惠顾”不赠购物券;如果顾客不愿意抽奖,可以直接获得购物券10元,小明购买了100元的商品,他看到商场公布的前10000张奖券的抽奖结果如下:
奖券种类
紫气东来
化开富贵
吉星高照
谢谢惠顾
出现张数(张)
500
1000
2000
6500
(1)求“紫气东来”奖券出现的频率;
(2)请你帮助小明判断,抽奖和直接获得购物券,哪种方式更合算?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=(x﹣1)2+2沿x轴向右平移2个单位后,再沿y轴向下平移3个单位,得到的抛物线解析式为( )
A.y=(x﹣3)2+1B.y=(x+1)2﹣1C.y=(x﹣3)2﹣1D.y=(x+1)2﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣x2+1向右平移2个单位长度,再向下平移3个长度单位得到的抛物线解析式是( )
A.y=﹣(x﹣2)2+4B.y=﹣(x﹣2)2﹣2
C.y=﹣(x+2)2+4D.y=﹣(x+2)2﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】点(3,2)关于x轴的对称点为( )
A. (3,-2) B. (-3,2) C. (-3,-2) D. (2,-3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+3x+m=0有一个根为﹣2,则m=_____,另一个根为_____.
相关试题

