【题目】如图,在△ABC中,AC=50 cm,BC=40 cm,∠C=90°,点P从点A开始沿AC边向点C以2 cm/s的速度匀速运动,同时另一点Q由点C开始以3 cm/s的速度沿着CB向点B匀速运动,当其中一点到达终点时,另一点也随之停止运动,则当△PCQ的面积等于300 cm2时,运动时间为( )

A. 5 s B. 20 s C. 5 s或20 s D. 不确定
参考答案:
【答案】A
【解析】设x秒后,△PCQ的面积等于300 cm2,根据路程=速度×时间,可用时间x表示出CP和CQ的长,然后根据直角三角形的面积公式,得出方程,求出未知数,然后看看解是否符合题意,将不合题意的舍去,即可得出时间的值.
设x秒后,△PCQ的面积等于300 cm2,有:![]() (50-2x)×3x=300,
(50-2x)×3x=300,
∴x2-25x+100=0,
∴x1=5,x2=20.
当x=20s时,CQ=3x=3×20=60>BC=40,即x=20s不合题意,舍去.
答:5秒后,△PCQ的面积等于300 cm2.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设
 ,
, .
.①如图2,当点在线段BC上移动,则
 ,
, 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;②当点在直线BC上移动,则
 ,
, 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中:①PA=PB;②△AOP≌△BOP;③OA=OB;④PO平分∠APB.其中成立的有________(填写正确的序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=﹣
 x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.
x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.(1)当t=
 秒时,点Q的坐标是 ;
秒时,点Q的坐标是 ;(2)在运动过程中,设正方形PQMN与△AOB重叠部分的面积为S,求S与t的函数表达式;
(3)若正方形PQMN对角线的交点为T,请直接写出在运动过程中OT+PT的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:(1)3x2-5x+2=0;(2)(7x+3)2=2(7x+3);
(3)t2-
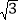 t-
t-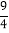 =0;(4)(y+1)(y-1)=2y-1.
=0;(4)(y+1)(y-1)=2y-1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,四边形 OABC 为菱形,对角线 OB、AC 相交于 D 点,已知 A点的坐标为(10,0),双曲线 y=
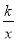 ( x>0 )经过 D 点,交 BC 的延长线于 E 点,且 OBAC=120(OB>AC),有下列四个结论:①双曲线的解析式为y=
( x>0 )经过 D 点,交 BC 的延长线于 E 点,且 OBAC=120(OB>AC),有下列四个结论:①双曲线的解析式为y=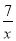 (x>0);②E 点的坐标是(4,6);③sin∠COA=
(x>0);②E 点的坐标是(4,6);③sin∠COA=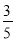 ;④EC=
;④EC=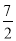 ;⑤AC+OB=8
;⑤AC+OB=8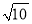 .其中正确的结论有( )
.其中正确的结论有( )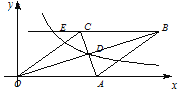
A. 4 个 B. 3 个 C. 2 个 D. 1 个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
 的图象与y轴正半轴相交,其顶点坐标为(
的图象与y轴正半轴相交,其顶点坐标为( ,1),下列结论:①abc>0;②a=b;③a=4c﹣4;④方程
,1),下列结论:①abc>0;②a=b;③a=4c﹣4;④方程 有两个相等的实数根,其中正确的结论是______.(只填序号即可).
有两个相等的实数根,其中正确的结论是______.(只填序号即可).
相关试题

