【题目】如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中:①PA=PB;②△AOP≌△BOP;③OA=OB;④PO平分∠APB.其中成立的有________(填写正确的序号).

参考答案:
【答案】①②③④
【解析】
根据角平分线上的点到角的两边距离相等可得PA=PB,再利用“HL”证明△AOP和△BOP全等,根据全等三角形对应边相等可得OA=OB,全等三角形对应角相等可得∠APO=∠BPO,即可得到PO平分∠APB.
解:∵OP平分∠AOB,PA⊥OA,PB⊥OB,
∴PA=PB,故①正确;
在△AOP和△BOP中,![]() ,
,
∴△AOP≌△BOP(HL),故②正确;
∴∠APO=∠BPO,OA=OB,故③正确;
∴PO平分∠APB,故④正确;
故答案为:①②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】元旦是公历新一年的第一天.“元旦”一词最早出现于《晋书》:“颛帝以孟夏正月为元,其实正朔元旦之春.”中国古代曾以腊月、十月等的月首为元旦,1949年中华人民共和国以公历1月1日为元旦,因此元旦在中国也被称为“阳历年”.为庆祝元旦,太原某商场举行促销活动,促销的方法是“消费超过200元时,所购买的商品按原价打8折后,再减少20元”.若某商品的原价为
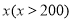 元,则购买该商品实际付款的金额是( )
元,则购买该商品实际付款的金额是( )A.
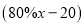 元B.
元B.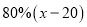 元C.
元C.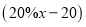 元D.
元D.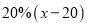 元
元 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=CB,AD=CD,对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E、F.求证:OE=OF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设
 ,
, .
.①如图2,当点在线段BC上移动,则
 ,
, 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;②当点在直线BC上移动,则
 ,
, 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=﹣
 x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.
x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.(1)当t=
 秒时,点Q的坐标是 ;
秒时,点Q的坐标是 ;(2)在运动过程中,设正方形PQMN与△AOB重叠部分的面积为S,求S与t的函数表达式;
(3)若正方形PQMN对角线的交点为T,请直接写出在运动过程中OT+PT的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=50 cm,BC=40 cm,∠C=90°,点P从点A开始沿AC边向点C以2 cm/s的速度匀速运动,同时另一点Q由点C开始以3 cm/s的速度沿着CB向点B匀速运动,当其中一点到达终点时,另一点也随之停止运动,则当△PCQ的面积等于300 cm2时,运动时间为( )

A. 5 s B. 20 s C. 5 s或20 s D. 不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:(1)3x2-5x+2=0;(2)(7x+3)2=2(7x+3);
(3)t2-
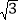 t-
t-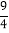 =0;(4)(y+1)(y-1)=2y-1.
=0;(4)(y+1)(y-1)=2y-1.
相关试题

