【题目】如图,在平面直角坐标系中,一次函数y=﹣![]() x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.
x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.
(1)当t=![]() 秒时,点Q的坐标是 ;
秒时,点Q的坐标是 ;
(2)在运动过程中,设正方形PQMN与△AOB重叠部分的面积为S,求S与t的函数表达式;
(3)若正方形PQMN对角线的交点为T,请直接写出在运动过程中OT+PT的最小值.

参考答案:
【答案】(1)(4,0);(2)①当0<t≤1时,S =![]() t2;②当1<t≤
t2;②当1<t≤![]() 时,S =﹣
时,S =﹣![]() t2+18t;③当
t2+18t;③当![]() <t≤2时, S =﹣3t2+12;(3)OT+PT的最小值为
<t≤2时, S =﹣3t2+12;(3)OT+PT的最小值为![]() .
.
【解析】(1)先确定出点A的坐标,进而求出AP,利用对称性即可得出结论;
(2)分三种情况,①利用正方形的面积减去三角形的面积,②利用矩形的面积减去三角形的面积,③利用梯形的面积,即可得出结论;
(3)先确定出点T的运动轨迹,进而找出OT+PT最小时的点T的位置,即可得出结论.
(1)令y=0,
∴﹣![]() x+4=0,
x+4=0,
∴x=6,
∴A(6,0),
当t=![]() 秒时,AP=3×
秒时,AP=3×![]() =1,
=1,
∴OP=OA﹣AP=5,
∴P(5,0),
由对称性得,Q(4,0);
(2)当点Q在原点O时,OQ=6,
∴AP=![]() OQ=3,
OQ=3,
∴t=3÷3=1,
①当0<t≤1时,如图1,令x=0,
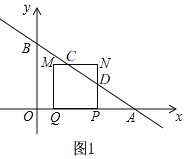
∴y=4,
∴B(0,4),
∴OB=4,
∵A(6,0),
∴OA=6,
在Rt△AOB中,tan∠OAB=![]() ,
,
由运动知,AP=3t,
∴P(6﹣3t,0),
∴Q(6﹣6t,0),
∴PQ=AP=3t,
∵四边形PQMN是正方形,
∴MN∥OA,PN=PQ=3t,
在Rt△APD中,tan∠OAB=![]() ,
,
∴PD=2t,
∴DN=t,
∵MN∥OA
∴∠DCN=∠OAB,
∴tan∠DCN=![]() ,
,
∴CN=![]() t,
t,
∴S=S正方形PQMN﹣S△CDN=(3t)2﹣![]() t×
t×![]() t=
t=![]() t2;
t2;
②当1<t≤![]() 时,如图2,同①的方法得,DN=t,CN=
时,如图2,同①的方法得,DN=t,CN=![]() t,
t,
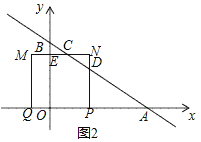
∴S=S矩形OENP﹣S△CDN=3t×(6﹣3t)﹣![]() t×
t×![]() t=﹣
t=﹣![]() t2+18t;
t2+18t;
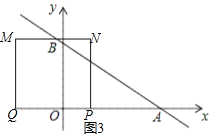
③当![]() <t≤2时,如图3,S=S梯形OBDP=
<t≤2时,如图3,S=S梯形OBDP=![]() (2t+4)(6﹣3t)=﹣3t2+12;
(2t+4)(6﹣3t)=﹣3t2+12;
(3)如图4,由运动知,P(6﹣3t,0),Q(6﹣6t,0),
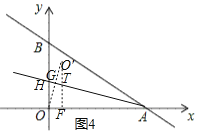
∴M(6﹣6t,3t),
∵T是正方形PQMN的对角线交点,
∴T(6﹣![]() t,
t,![]() t)
t)
∴点T是直线y=﹣![]() x+2上的一段线段,(﹣3≤x<6),
x+2上的一段线段,(﹣3≤x<6),
作出点O关于直线y=﹣![]() x+2的对称点O'交此直线于G,过点O'作O'F⊥x轴,则O'F就是OT+PT的最小值,
x+2的对称点O'交此直线于G,过点O'作O'F⊥x轴,则O'F就是OT+PT的最小值,
由对称知,OO'=2OG,
易知,OH=2,
∵OA=6,AH=![]() ,
,
∴S△AOH=![]() OH×OA=
OH×OA=![]() AH×OG,
AH×OG,
∴OG=![]() ,
,
∴OO'=![]()
在Rt△AOH中,sin∠OHA=![]() ,
,
∵∠HOG+∠AOG=90°,∠HOG+∠OHA=90°,
∴∠AOG=∠OHA,
在Rt△OFO'中,O'F=OO'sin∠O'OF=![]() ×
×![]() =
=![]() ,
,
即:OT+PT的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=CB,AD=CD,对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E、F.求证:OE=OF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设
 ,
, .
.①如图2,当点在线段BC上移动,则
 ,
, 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;②当点在直线BC上移动,则
 ,
, 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中:①PA=PB;②△AOP≌△BOP;③OA=OB;④PO平分∠APB.其中成立的有________(填写正确的序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=50 cm,BC=40 cm,∠C=90°,点P从点A开始沿AC边向点C以2 cm/s的速度匀速运动,同时另一点Q由点C开始以3 cm/s的速度沿着CB向点B匀速运动,当其中一点到达终点时,另一点也随之停止运动,则当△PCQ的面积等于300 cm2时,运动时间为( )

A. 5 s B. 20 s C. 5 s或20 s D. 不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:(1)3x2-5x+2=0;(2)(7x+3)2=2(7x+3);
(3)t2-
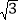 t-
t-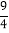 =0;(4)(y+1)(y-1)=2y-1.
=0;(4)(y+1)(y-1)=2y-1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,四边形 OABC 为菱形,对角线 OB、AC 相交于 D 点,已知 A点的坐标为(10,0),双曲线 y=
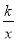 ( x>0 )经过 D 点,交 BC 的延长线于 E 点,且 OBAC=120(OB>AC),有下列四个结论:①双曲线的解析式为y=
( x>0 )经过 D 点,交 BC 的延长线于 E 点,且 OBAC=120(OB>AC),有下列四个结论:①双曲线的解析式为y=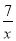 (x>0);②E 点的坐标是(4,6);③sin∠COA=
(x>0);②E 点的坐标是(4,6);③sin∠COA=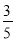 ;④EC=
;④EC=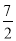 ;⑤AC+OB=8
;⑤AC+OB=8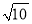 .其中正确的结论有( )
.其中正确的结论有( )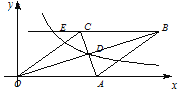
A. 4 个 B. 3 个 C. 2 个 D. 1 个
相关试题

