Question

【题目】在平面直角坐标系中，A点坐标为（3，4），将线段OA绕原点O逆时针旋转90°得到线段OA′，则点A′的坐标是（ ）
A.（﹣4，3）
B.（﹣3，4）
C.（3，﹣4）
D.（4，﹣3）

Answer 1

【答案】A
【解析】解：如图，过点A作AB⊥x轴于B，过点A′作A′B′⊥x轴于B′，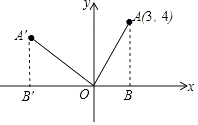

∵OA绕坐标原点O逆时针旋转90°至OA′，
∴OA=OA′，∠AOA′=90°，
∵∠A′OB′+∠AOB=90°，∠AOB+∠OAB=90°，
∴∠OAB=∠A′OB′，
在△AOB和△OA′B′中，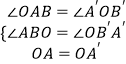
，
∴△AOB≌△OA′B′（AAS），
∴OB′=AB=4，A′B′=OB=3，
∴点A′的坐标为（﹣4，3）．
故选：A．
【考点精析】解答此题的关键在于理解旋转的性质的相关知识，掌握①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了．