【题目】某商店销售面向中考生的计数跳绳,每根成本为20元,销售的前40天内的日销售量m(根)与时间t(天)的关系如表.
时间t(天) | 1 | 3 | 8 | 10 | 26 | … |
日销售量m(件) | 51 | 49 | 44 | 42 | 26 | … |
前20天每天的价格y1(元/件)与时间t(天)的函数关系式为:y1= ![]() t+25(1≤t≤20且t为整数);后20天每天的价格y2(元/件)与时间t(天)的函数关系式为:y2=﹣
t+25(1≤t≤20且t为整数);后20天每天的价格y2(元/件)与时间t(天)的函数关系式为:y2=﹣ ![]() t+40(21≤t≤40且t为整数).
t+40(21≤t≤40且t为整数).
(1)认真分析表中的数据,用所学过的一次函数,二次函数的知识确定一个满足这些数据m(件)与t(天)之间的关系式;
(2)请计算40天中娜一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<3)给希望工程,公司通过销售记录发现,前20天中扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
参考答案:
【答案】
(1)解:由表格中数据可知,当时间t每增加1天,日销售量相应减少1件,
∴m与t满足一次函数关系,
设m=kt+b,将(1,51)、(3,49)代入,
得: ![]() ,
,
解得: ![]() ,
,
∴m与t的函数关系为:m=﹣t+52
(2)解:设日销售利润为P,
当1≤t≤20时,
P=(﹣t+52)( ![]() t+25﹣20)=﹣
t+25﹣20)=﹣ ![]() (t﹣16)2+324,
(t﹣16)2+324,
∴当t=16时,P有最大值,最大值为324元;
当21≤t≤40时,
P=(﹣t+52)(﹣ ![]() t+40﹣20)=
t+40﹣20)= ![]() (t﹣46)2﹣18,
(t﹣46)2﹣18,
∵当t<46时,P随t的增大而减小,
∴当t=21时,P取得最大值,最大值为 ![]() (21﹣46)2﹣18=294.5元;
(21﹣46)2﹣18=294.5元;
∵324>294.5,
∴第16天时,销售利润最大,最大利润为324元
(3)解:设前20天扣除捐赠后的日利润为W,
则W=(﹣t+52)( ![]() t+25﹣20﹣a)=﹣
t+25﹣20﹣a)=﹣ ![]() [t﹣2(8+a)]2+a2﹣36a+324,
[t﹣2(8+a)]2+a2﹣36a+324,
∴对称轴为t=16+2a,
∵1≤t≤20,
∴16+2a≥20,解得:a≥2,
即a≥2时,W随t的增大而增大,
又∵a<3,
∴2≤a<3
【解析】(1)从表格可看出每天比前一天少销售1件,所以判断为一次函数关系式,待定系数法求解可得解析式;(2)日利润=日销售量×每件利润,据此分别表示前20天和后20天的日利润,根据函数性质求最大值后比较得出结论;(3)列式表示前20天中每天扣除捐赠后的日销售利润,根据函数性质求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形
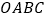 的顶点
的顶点 在坐标原点,顶点
在坐标原点,顶点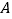 在
在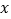 轴上,
轴上,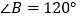 ,
,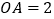 .将菱形
.将菱形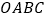 绕原点顺时针旋转105至
绕原点顺时针旋转105至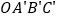 的位置,则点
的位置,则点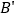 的坐标为( )
的坐标为( )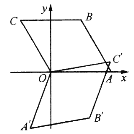
A.
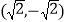 B.
B. 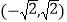 C.
C. 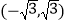 D.
D. 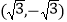
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是____________。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B+∠D=180°,AB=AD,AC=1,∠ACD=60°,求四边形ABCD的面积.
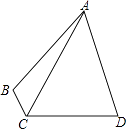
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 为原点,四边形
为原点,四边形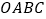 是长方形,点
是长方形,点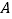 ,
,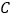 的坐标分别为
的坐标分别为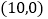 ,
,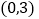 ,
,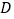 是
是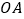 的中点,点
的中点,点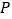 在边
在边 上运动,当
上运动,当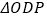 是腰长为5的等腰三角形时,点
是腰长为5的等腰三角形时,点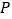 的坐标为_______.
的坐标为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.
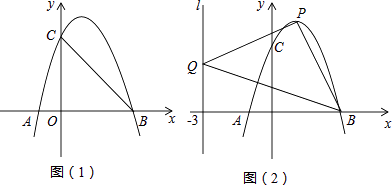
(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
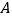 ,
,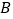 的坐标分别为
的坐标分别为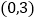 ,
,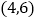 ,点
,点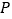 是
是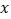 轴上的一个动点,若点
轴上的一个动点,若点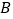 关于直线
关于直线 的对称点
的对称点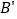 恰好落在坐标轴上,则点
恰好落在坐标轴上,则点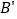 的坐标为_______.
的坐标为_______. 
相关试题

