【题目】如图,某人在山坡坡脚C处测得一座建筑物顶点A的仰角为60°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为45°.已知BC=90米,且B、C、D在同一条直线上,山坡坡度为 ![]() (即tan∠PCD=
(即tan∠PCD= ![]() ).
).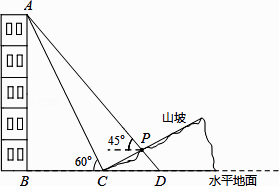
(1)求该建筑物的高度(即AB的长).
(2)求此人所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
参考答案:
【答案】
(1)
解:过点P作PE⊥BD于E,PF⊥AB于F,
又∵AB⊥BC于B,
∴四边形BEPF是矩形,
∴PE=BF,PF=BE
∵在Rt△ABC中,BC=90米,∠ACB=60°,
∴AB=BCtan60°=90 ![]() (米),
(米),
故建筑物的高度为90 ![]() 米;
米;
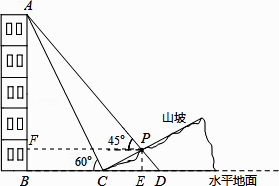
(2)
解:设PE=x米,则BF=PE=x米,
∵在Rt△PCE中,tan∠PCD= ![]() =
= ![]() ,
,
∴CE=2x,
∵在Rt△PAF中,∠APF=45°,
∴AF=AB﹣BF=90 ![]() ﹣x,
﹣x,
PF=BE=BC+CE=90+2x,
又∵AF=PF,
∴90 ![]() ﹣x=90+2x,
﹣x=90+2x,
解得:x=30 ![]() ﹣30,
﹣30,
答:人所在的位置点P的铅直高度为( ![]() )米
)米
【解析】(1)过点P作PE⊥BD于E,PF⊥AB于F,在Rt△ABC中,求出AB的长度即可;(2)设PE=x米,则BF=PE=x米,根据山坡坡度为 ![]() ,用x表示CE的长度,然后根据AF=PF列出等量关系式,求出x的值即可.
,用x表示CE的长度,然后根据AF=PF列出等量关系式,求出x的值即可.
【考点精析】本题主要考查了关于仰角俯角问题的相关知识点,需要掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,
组别
课堂发言次数n
A
0≤n<3
B
3≤n<6
C
6≤n<9
D
9≤n<12
E
12≤n<15
F
15≤n<18
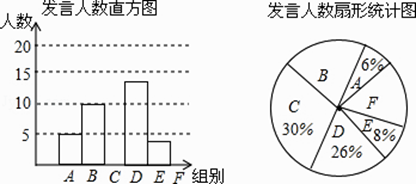
请结合图中相关数据回答下列问题:
(1)样本容量是 , 并补全直方图;
(2)该年级共有学生800人,请估计该年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰好有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好都是男生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边三角形AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,连接DA并延长,交y轴于点E.
①△OBC与△ABD全等吗?判断并证明你的结论;
②当点C运动到什么位置时,以A,E,C为顶点的三角形是等腰三角形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
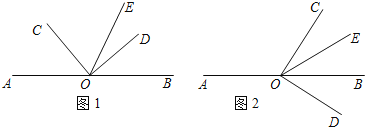
(1)如图(1),若∠AOC=
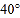 ,求∠DOE的度数;
,求∠DOE的度数;(2)如图(2),将∠COD绕顶点O旋转,且保持射线OC在直线AB上方,在整个旋转过程中,当∠AOC的度数是多少时,∠COE=2∠DOB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠BAC=90°,D是AC的中点,CE⊥BD于点E,交BA的延长线于点F.若BF=12,则△FBC的面积为( )

A. 40 B. 46 C. 48 D. 50
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作
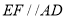 ,与AC、DC分别交于点
,与AC、DC分别交于点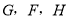 为CG的中点,连结DE、EH、DH、
为CG的中点,连结DE、EH、DH、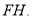 下列结论:
下列结论: 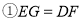 ;
; 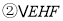 ≌
≌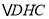 ;
; 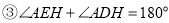 ;
;  若
若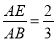 ,则
,则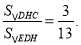 其中结论正确的有
其中结论正确的有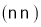
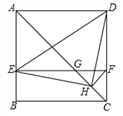
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是
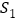 、
、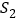 、
、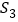 、
、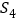 ,则
,则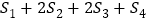 =( )
=( )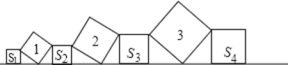
A. 5 B. 4 C. 6 D. 、10
相关试题

