【题目】如图,在![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的平分线,
的平分线,![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,结论①
,结论①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )

A.4个B.3个C.2个D.1个
参考答案:
【答案】B
【解析】
①根据三角形的内角和定理判定∠CAM=∠CMA,由等腰三角形的判定和三线合一的性质可得结论正确;
②根据BN=AB=6,CM=AC=5,及线段的和与差可得BC的长;
③根据三角形的内角和定理及角的和与差可得结论;
④要想得到AM=AN,必有∠AMN=∠ANM,而AB≠AC,可知∠ABC≠∠ACB,从而得AM≠AN.
解:①∵CE平分∠ACE,
∴∠ACP=∠MCP,
∵AM⊥CE,
∴∠APC=∠MPC=90°,
∴∠CAM=∠CMA,
∴AC=CM,
∴AP=PM,
①正确;
②同理得:BN=AB=6,
∵CM=AC=5,
∴BC=BN+CM-MN=6+5-2=9,
②正确;
③∵∠BAC=∠MAC+∠BAN-∠MAN=110°,
由①知:∠CMA=∠CAM,∠BNA=∠BAN,
△AMN中,∠CMA+∠BNA=180°-∠MAN=∠BAN+∠MAC,
∴180°-∠MAN-∠MAN=110°,
∴∠MAN=35°,
③正确;
④当∠AMN=∠ANM时,AM=AN,
∵AB=6≠AC=5
∴∠ABC≠∠ACB,
∴∠AMN≠∠ANM,则AM与AN不相等,
④不正确;
所以本题不正确的有④,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有长为
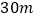 的篱笆,一面利用墙(墙的最大可用长度为
的篱笆,一面利用墙(墙的最大可用长度为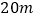 ),围成中间隔有一道篱笆(平行于
),围成中间隔有一道篱笆(平行于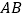 )的矩形花圃
)的矩形花圃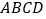 .设花圃的一边
.设花圃的一边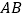 为
为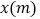 .
.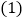 则
则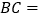 ________(用含
________(用含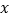 的代数式表示),矩形
的代数式表示),矩形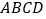 的面积
的面积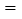 ________(用含
________(用含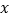 的代数式表示);
的代数式表示);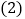 如果要围成面积为
如果要围成面积为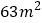 的花圃,
的花圃,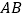 的长是多少?
的长是多少?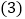 将
将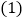 中表示矩形
中表示矩形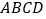 的面积的代数式通过配方,问:当
的面积的代数式通过配方,问:当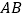 等于多少时,能够使矩形花圃
等于多少时,能够使矩形花圃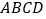 面积最大,最大的面积为多少?
面积最大,最大的面积为多少?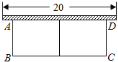
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,对称轴为
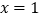 的抛物线
的抛物线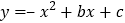 与
与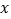 轴交于
轴交于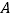 、
、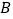 两点,与
两点,与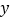 轴交于
轴交于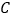 点,其中
点,其中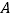 点坐标为
点坐标为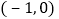 设抛物线的顶点为
设抛物线的顶点为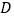 .
.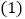 求抛物线的解析式及顶点坐标;
求抛物线的解析式及顶点坐标;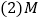 为
为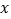 轴上的一点,当
轴上的一点,当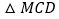 的周长最小时,求点
的周长最小时,求点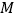 的坐标及
的坐标及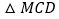 的周长.
的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批衬衫,平均每天可售出
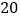 件,每件盈利
件,每件盈利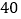 元.为了扩大销售,增加盈利,商场决定采取适当的降价措施.经调查发现,在一定范围内,衬衫的单价每下降
元.为了扩大销售,增加盈利,商场决定采取适当的降价措施.经调查发现,在一定范围内,衬衫的单价每下降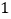 元,商场平均每天可多售出
元,商场平均每天可多售出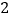 件.
件. 如果商场通过销售这批衬衫每天获利
如果商场通过销售这批衬衫每天获利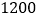 元,那么衬衫的单价应下降多少元?
元,那么衬衫的单价应下降多少元? 当每件衬衫的单价下降多少元时,每天通过销售衬衫获得的利润最大?最大利润为多少元?
当每件衬衫的单价下降多少元时,每天通过销售衬衫获得的利润最大?最大利润为多少元? -
科目: 来源: 题型:
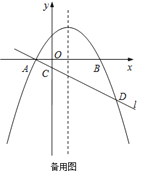
查看答案和解析>>【题目】如图,在平面直角坐标系
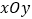 中,抛物线
中,抛物线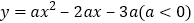 与
与 轴交于
轴交于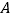 ,
,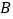 两点(点
两点(点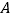 在点
在点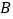 的左侧),经过点
的左侧),经过点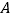 的直线
的直线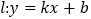 与
与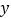 轴交于点
轴交于点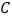 ,与抛物线的另一个交点为
,与抛物线的另一个交点为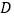 ,且
,且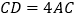 .
.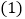 直接写出点
直接写出点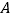 的坐标,并求直线
的坐标,并求直线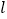 的函数表达式(其中
的函数表达式(其中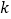 ,
, 用含
用含 的式子表示);
的式子表示);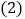 点
点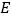 是直线
是直线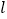 上方的抛物线上的一点,若
上方的抛物线上的一点,若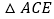 的面积的最大值为
的面积的最大值为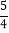 ,求
,求 的值;
的值; 设
设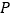 是抛物线对称轴上的一点,点
是抛物线对称轴上的一点,点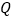 在抛物线上,以点
在抛物线上,以点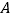 ,
,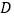 ,
,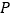 ,
,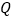 为顶点的四边形能否成为矩形?若能,求出点
为顶点的四边形能否成为矩形?若能,求出点 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.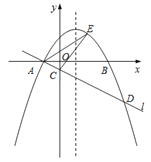
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC=16 cm,AD为BC边上的高,动点P从点A出发,沿A→D方向以
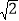 cm/s的速度向点D运动,过P点作矩形PDFE(E点在AC上),设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒(0<t<8).
cm/s的速度向点D运动,过P点作矩形PDFE(E点在AC上),设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒(0<t<8).(1)经过几秒钟后,S1=S2?
(2)经过几秒钟后,S1+S2最大?并求出这个最大值.
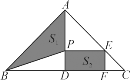
-
科目: 来源: 题型:
查看答案和解析>>【题目】在长方形纸片ABCD中,AB=m,AD=n,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.

(1)在图1中,EF=___,BF=____;(用含m的式子表示)
(2)请用含m、n的式子表示图1,图2中的S1,S2,若m-n=2,请问S2-S1的值为多少?
相关试题

