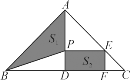
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC=16 cm,AD为BC边上的高,动点P从点A出发,沿A→D方向以![]() cm/s的速度向点D运动,过P点作矩形PDFE(E点在AC上),设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒(0<t<8).
cm/s的速度向点D运动,过P点作矩形PDFE(E点在AC上),设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒(0<t<8).
(1)经过几秒钟后,S1=S2?
(2)经过几秒钟后,S1+S2最大?并求出这个最大值.
参考答案:
【答案】(1) t=4 (2) t=6
【解析】
分别根据运动方式列出面积S1,S2关于t的函数关系,第一问令面积相等,第二问配方求最值.
解:S1=![]() ×8
×8![]() ×
×![]() t=8t,S2=
t=8t,S2=![]() t(8
t(8![]() -
-![]() t)=-2t2+16t,(1)由8t=-2t2+16t,解得t1=4,t2=0(舍去),∴当t=4秒时,S1=S2
t)=-2t2+16t,(1)由8t=-2t2+16t,解得t1=4,t2=0(舍去),∴当t=4秒时,S1=S2
(2)∵S1+S2=8t+(-2t2+16t)=-2(t-6)2+72,∴当t=6时,S1+S2最大,最大为72
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批衬衫,平均每天可售出
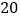 件,每件盈利
件,每件盈利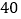 元.为了扩大销售,增加盈利,商场决定采取适当的降价措施.经调查发现,在一定范围内,衬衫的单价每下降
元.为了扩大销售,增加盈利,商场决定采取适当的降价措施.经调查发现,在一定范围内,衬衫的单价每下降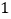 元,商场平均每天可多售出
元,商场平均每天可多售出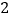 件.
件.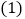 如果商场通过销售这批衬衫每天获利
如果商场通过销售这批衬衫每天获利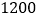 元,那么衬衫的单价应下降多少元?
元,那么衬衫的单价应下降多少元? 当每件衬衫的单价下降多少元时,每天通过销售衬衫获得的利润最大?最大利润为多少元?
当每件衬衫的单价下降多少元时,每天通过销售衬衫获得的利润最大?最大利润为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 、
、 分别是
分别是 和
和 的平分线,
的平分线, 于
于 ,交
,交 于
于 ,
, 于
于 ,交
,交 于
于 ,
, ,
, ,
,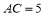 ,
, ,结论①
,结论① ;②
;② ;③
;③ ;④
;④ .其中正确的有( )
.其中正确的有( )
A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
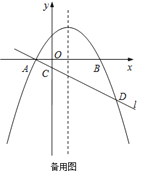
查看答案和解析>>【题目】如图,在平面直角坐标系
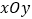 中,抛物线
中,抛物线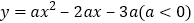 与
与 轴交于
轴交于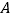 ,
,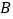 两点(点
两点(点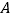 在点
在点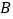 的左侧),经过点
的左侧),经过点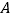 的直线
的直线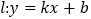 与
与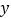 轴交于点
轴交于点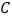 ,与抛物线的另一个交点为
,与抛物线的另一个交点为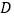 ,且
,且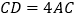 .
.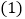 直接写出点
直接写出点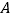 的坐标,并求直线
的坐标,并求直线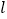 的函数表达式(其中
的函数表达式(其中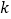 ,
, 用含
用含 的式子表示);
的式子表示);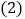 点
点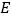 是直线
是直线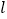 上方的抛物线上的一点,若
上方的抛物线上的一点,若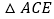 的面积的最大值为
的面积的最大值为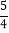 ,求
,求 的值;
的值; 设
设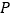 是抛物线对称轴上的一点,点
是抛物线对称轴上的一点,点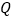 在抛物线上,以点
在抛物线上,以点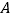 ,
,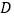 ,
,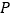 ,
,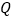 为顶点的四边形能否成为矩形?若能,求出点
为顶点的四边形能否成为矩形?若能,求出点 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.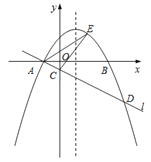
-
科目: 来源: 题型:
查看答案和解析>>【题目】在长方形纸片ABCD中,AB=m,AD=n,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.

(1)在图1中,EF=___,BF=____;(用含m的式子表示)
(2)请用含m、n的式子表示图1,图2中的S1,S2,若m-n=2,请问S2-S1的值为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求证:无论m取何值,原方程总有两个不相等的实数根;
(2)若x1,x2是原方程的两根,且|x1-x2|=2
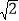 ,求m的值.
,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】中秋节前夕,某超市采购了一批土特产,根据以往销售经验,每天的售价与销售量之间有如下表的关系:
每千克售价(元)
38
37
36
35
…
20
每天销售量(千克)
50
52
54
56
…
86
设当售价从38元/千克下调到x元/千克时,销售量为y千克.
(1)根据上述表格中提供的数据,通过在直角坐标系中描点连线等方法,猜测并求出y与x之间的函数解析式;
(2)如果这种土特产的成本价是20元/千克,为使某一天的利润为780元,那么这一天每千克的售价应为多少元?(利润=销售总金额-成本)
相关试题

