【题目】正方形ABCD中,将一个直角三角板的直角顶点与点A重合,一条直角边与边BC交于点E(点E不与点B和点C重合),另一条直角边与边CD的延长线交于点F. 
(1)如图①,求证:AE=AF;
(2)如图②,此直角三角板有一个角是45°,它的斜边MN与边CD交于G,且点G是斜边MN的中点,连接EG,求证:EG=BE+DG;
(3)在(2)的条件下,如果 ![]() =
= ![]() ,那么点G是否一定是边CD的中点?请说明你的理由.
,那么点G是否一定是边CD的中点?请说明你的理由.
参考答案:
【答案】
(1)解:如图①,∵四边形ABCD是正方形,
∴∠B=∠BAD=∠ADC=∠C=90°,AB=AD.
∵∠EAF=90°,
∴∠EAF=∠BAD,
∴∠EAF﹣∠EAD=∠BAD﹣∠EAD,
∴∠BAE=∠DAF.
在△ABE和△ADF中
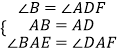 ,
,
∴△ABE≌△ADF(ASA)
∴AE=AF
(2)解:如图②,连接AG,
∵∠MAN=90°,∠M=45°,
∴∠N=∠M=45°,
∴AM=AN.
∵点G是斜边MN的中点,
∴∠EAG=∠NAG=45°.
∴∠EAB+∠DAG=45°.
∵△ABE≌△ADF,
∴∠BAE=∠DAF,AE=AF,
∴∠DAF+∠DAG=45°,
即∠GAF=45°,
∴∠EAG=∠FAG.
在△AGE和AGF中,
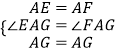 ,
,
∴△AGE≌AGF(SAS),
∴EG=GF.
∵GF=GD+DF,
∴GF=GD+BE,
∴EG=BE+DG
(3)解:G不一定是边CD的中点.
理由:设AB=6k,GF=5k,BE=x,
∴CE=6k﹣x,EG=5k,CF=CD+DF=6k+x,
∴CG=CF﹣GF=k+x,
在Rt△ECG中,由勾股定理,得
(6k﹣x)2+(k+x)2=(5k)2,
解得:x1=2k,x2=3k,
∴CG=4k或3k.
∴点G不一定是边CD的中点.
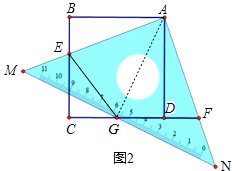
【解析】(1)由正方形的性质可以得出∠B=∠BAD=∠ADC=∠C=90°,AB=AD,由直角三角形的性质∠EAF=∠BAD=90°,就可以得出∠BAE=∠DAF,证明△ABE≌△ADF就可以得出结论;(2)如图2,连结AG,由且点G是斜边MN的中点,△AMN是等腰直角三角形,就可以得出∠EAG=∠NAG=45°,就有∠EAB+∠DAG=45°,由△ABE≌△ADF可以得出∠BAE=∠DAF,AE=AF就可以得出△AGE≌AGF,从而得出结论;(3)设AB=6k,GF=5k,BE=x,就可以得出CE=6k﹣x,EG=5k,CF=CD+DF=6k+x,就有CG=CF﹣GF=k+x,由勾股定理就可以x的值而得出结论.
【考点精析】掌握正方形的性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
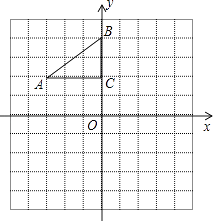
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利过程.下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:

(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润是多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】长城科技公司生产销售一种电子产品,该产品总成本包括技术成本、制造成本、销售成本三部分,经核算,2014年该产品各部分成本所占比例约为2:a:1.且2014年该产品的技术成本、制造成本分别为400万元、1400万元.
(1)确定a的值,并求2014年产品总成本为多少万元;
(2)为降低总成本,该公司2015年及2016年增加了技术成本投入,确保这两年技术成本都比前一年增加一个相同的百分数m(m<50%),制造成本在这两年里都比前一年减少一个相同的百分数2m;同时为了扩大销售量,2016年的销售成本将在2014年的基础上提高10%,经过以上变革,预计2016年该产品总成本达到2014年该产品总成本的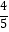 ,求m的值.
,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上(点A与点B不重合),我们定义:这样的两条抛物L1 , L2互为“友好”抛物线,可见一条抛物线的“友好”抛物线可以有多条.

(1)如图2,已知抛物线L3:y=2x2﹣8x+4与y轴交于点C,试求出点C关于该抛物线对称轴对称的点D的坐标;
(2)请求出以点D为顶点的L3的友好抛物线L4的解析式,并指出L3与L4中y同时随x增大而增大的自变量的取值范围;
(3)若抛物y=a1 (x﹣m)2+n的任意一条友好抛物线的解析式为y=a2 (x﹣h)2+k,请写出a1与a2的关系式,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象与x轴交于(x1 , 0),(x2 , 0)两点,且0<x1<1,1<x2<2,与y轴交于(0,﹣2).下列结论:①2a+b>1; ②a+b>2;③a﹣b<2;④3a+b>0; ⑤a<﹣1.其中正确结论的个数为( )
A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AB=5,则CD= .

相关试题

