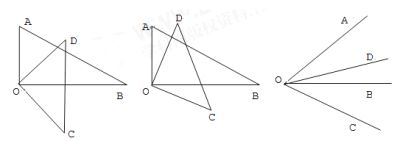
【题目】(1) 将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起, ∠AOB=∠DOC=90°.
①如图(1),若OD是∠AOB的平分线时,求∠BOD和∠AOC的度数.
②如图(2),若OD不是∠AOB的平分线,试猜想∠AOC与∠BOD的数量关系,并说明理由.
(2)如图(3),如果两个角∠AOB = ∠DOC= m°(0< m <90),直接写出∠AOC与∠BOD的数量关系.
参考答案:
【答案】(1)①45°;135°;②∠AOC+∠BOD=180°,理由见解析;(2)∠AOC+∠BOD=2 m° .
【解析】
(1)先根据角平分线的定义求出∠BOD,再求出∠BOC,然后根据∠AOC=∠AOB+∠BOC计算即可;
(2)根据∠BOC=∠DOC-∠BOD,∠AOC=∠AOB+∠BOC,整理即可得出答案;
(3)与(2)的步骤类似求解即可.
解: (1) ①因为∠AOB=90°, OD平分∠AOB,
所以![]() .
.
因为∠DOC=90° , ∠BOD=45°,
所以∠BOC=∠DOC-∠BOD=90°-45°=45°.
因为∠AOC=∠AOB+∠BOC,
所以∠AOC=90°+45°=135°;
②数量关系: ∠AOC+∠BOD=180°,
理由:∵∠BOC=∠DOC-∠BOD= 90°-∠BOD,
∠AOC=∠AOB+∠BOC,
∴∠AOC =90°+90°-∠BOD,
∴∠AOC+∠BOD=180° ;
(2) 关系: ∠AOC+∠BOD=2 m°.
理由:∵∠BOC=∠DOC-∠BOD= m°-∠BOD,
∠AOC=∠AOB+∠BOC,
∴∠AOC =m°+m°-∠BOD,
∴∠AOC+∠BOD=2m° ;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为

A.
 B.3 C.1 D.
B.3 C.1 D.
-
科目: 来源: 题型:
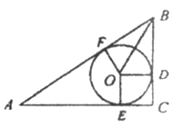
查看答案和解析>>【题目】如图,在△ABC中,已知∠C=90°,BC=3,AC=4,⊙O是内切圆,E,F,D分别为切点,则tan∠OBD的值为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是“用三角板画圆的切线”的画图过程.
如图1,已知圆上一点A,画过A点的圆的切线.
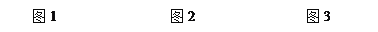

画法:(1)如图2,将三角板的直角顶点放在圆上任一点C(与点A不重合)处,使其一直角边经过点A,另一条直角边与圆交于B点,连接AB;
(2)如图3,将三角板的直角顶点与点A重合,使一条直角边经过点B,画出另一条直角边所在的直线AD.
所以直线AD就是过点A的圆的切线.
请回答:该画图的依据是_______________________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD为正方形,E是BC的中点,连接AE,过点A作∠AFD,使∠AFD=2∠EAB,AF交CD于点F,如图①,易证:AF=CD+CF.
(1)如图②,当四边形ABCD为矩形时,其他条件不变,线段AF,CD,CF之间有怎样的数量关系?请写出你的猜想,并给予证明;
(2)如图③,当四边形ABCD为平行四边形时,其他条件不变,线段AF,CD,CF之间又有怎样的数量关系?请直接写出你的猜想.
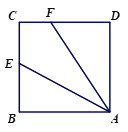
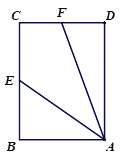
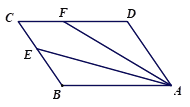
图① 图② 图③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AQ、BN、CN、DQ分別是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AQ与BN相交于点P,CN与DQ相交于点M,判断四边形MNPQ的形状,并证明你的结论.
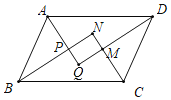
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y=
 (x>0)的图象与矩形OABC的边BC交于点D,分别过点A,D作AF∥DE,交直线y=k2x(k2<0)于点F,E.若OE=OF,BD=2CD,四边形ADEF的面积为12,则k1的值为________.
(x>0)的图象与矩形OABC的边BC交于点D,分别过点A,D作AF∥DE,交直线y=k2x(k2<0)于点F,E.若OE=OF,BD=2CD,四边形ADEF的面积为12,则k1的值为________. 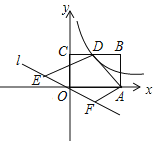
相关试题

