【题目】已知关于x的一元二次方程mx2+x+1=0.
(1)当该方程有一个根为1时,确定m的值;
(2)当该方程有两个不相等的实数根时,确定m的取值范围.
参考答案:
【答案】解:(1)把x=1代入mx2+x+1=0,得
m+1+1=0,
解得m=﹣2;
(2)由题意得:△=1﹣4m>0,
解得m<![]() .
.
又m≠0.
所以m的取值范围是:m<![]() 且m≠0.
且m≠0.
【解析】(1)把x=1代入已知方程,即利用方程的解进行解题;
(2)根据根的判别式得到:△>0,由此列出关于m的不等式,通过解不等式确定m的取值范围.
【考点精析】本题主要考查了求根公式的相关知识点,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2
 ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABM与△CDM是两个全等的等边三角形,MA⊥MD.有下列四个结论:(1)∠MBC=25°;(2)∠ADC+∠ABC=180°;(3)直线MB垂直平分线段CD;(4)四边形ABCD是轴对称图形.其中正确结论的个数为( )
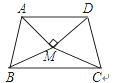
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,经过点A(-4,4)的抛物线y=ax2+bx+c与x轴相交于点B(-3,0)及原点O.
(1)求抛物线的解析式;
(2)如图1,过点A作AH⊥x轴,垂足为H,平行于y轴的直线交线段AO于点Q,交抛物线于点P,当四边形AHPQ为平行四边形时,求∠AOP的度数;
(3)如图2,若点C在抛物线上,且∠CAO=∠BAO,试探究:在(2)的条件下,是否存在点G,使得△GOP∽△COA?若存在,请求出所有满足条件的点G坐标;若不存在,请说明理由.
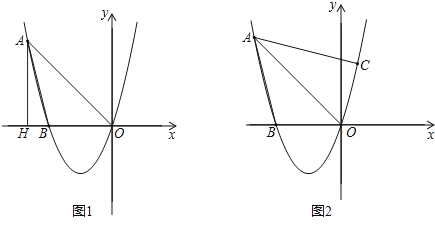
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=3x2的图象先向下平移3个单位,再向左平移4个单位所得的解析式为( )
A.y=3(x﹣3)2+4B.y=3(x+4)2﹣3
C.y=3(x﹣4)2+3D.y=3(x﹣4)2﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值不大于2015的所有整数的积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(﹣2,y1),B(﹣1,y2),C(3,y3)三点都在抛物线y=2x2﹣3的图象上,则y1,y2,y3的大小关系是( )
A.y3<y2<y1B.y1<y2<y3C.y2<y1<y3D.y3<y1<y2
相关试题

