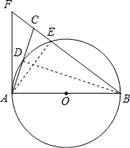
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.

参考答案:
【答案】(1)证明见试题解析;(2)CE=2,AF=![]() .
.
【解析】试题分析:(1)首先连接BD,由AB为直径,可得∠ADB=90°,又由AF是⊙O的切线,易证得∠CAF=∠ABD.然后由BA=BC,证得:∠ABC=2∠CAF;
(2)首先连接AE,设CE=x,由勾股定理可得方程:(2![]() )2=x2+(3x)2求得答案.
)2=x2+(3x)2求得答案.
试题解析:(1)证明:如图,连接BD.∵AB为⊙O的直径,∴∠ADB=90°,∴∠DAB+∠ABD=90°.∵AF是⊙O的切线,∴∠FAB=90°,即∠DAB+∠CAF=90°.∴∠CAF=∠ABD.∵BA=BC,∠ADB=90°,
∴∠ABC=2∠ABD.∴∠ABC=2∠CAF.
(2)如图,连接AE,∴∠AEB=90°,设CE=x,∵CE:EB=1:4,
∴EB=4x,BA=BC=5x,AE=3x,在Rt△ACE中,AC2=CE2+AE2,
即(2![]() )2=x2+(3x)2,∴x=2.∴CE=2.
)2=x2+(3x)2,∴x=2.∴CE=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线y=kx+b经过第二、三、四象限,则( )
A. k>0,b>0 B. k>0,b<0 C. k<0,b>0 D. k<0,b<0
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(
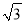 ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: 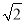 =1.41,
=1.41,  =1.73)
=1.73)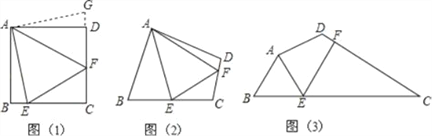
-
科目: 来源: 题型:
查看答案和解析>>【题目】为推进“传统文化进校园”活动,某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图(每人只能选择一个小组):
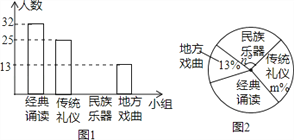
(1)报名参加课外活动小组的学生共有 人,将条形图补充完整;
(2)扇形图中m= ,n= ;
(3)根据报名情况,学校决定从报名“经典诵读”小组的甲、乙、丙、丁四人中随机安排两人到“地方戏曲”小组,甲、乙恰好都被安排到“地方戏曲”小组的概率是多少?请用列表或画树状图的方法说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于多项式﹣2ab2+3a3b+5﹣a2 , 下列说法中,正确的是( )
A.三次四项式
B.四次四项式
C.二次项系数是1
D.一次项是5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,斜面AC的坡度为1:2,AC=3
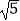 米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为( )
米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为( ) 
A.5米
B.6米
C.8米
D.(3+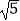 )米
)米 -
科目: 来源: 题型:
查看答案和解析>>【题目】某初一年级有500名同学,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),若要从身高在
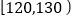 ,
, 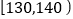 ,
, 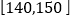 三组内的学生中,用分层抽样的方法选取30人参加一项活动,则从身高在
三组内的学生中,用分层抽样的方法选取30人参加一项活动,则从身高在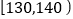 内的学生中选取的人数为_________.
内的学生中选取的人数为_________.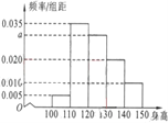
相关试题

