【题目】东东在研究数学问题时遇到一个定义:将三个已经排好顺序数:x1,x2,x3,称为数列x1,x2,x3.计算|x1|,![]() ,
,![]() ,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,
,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,![]() =
=![]() ,
,![]() =
=![]() ,所以数列2,-1,3的最佳值为
,所以数列2,-1,3的最佳值为![]() .
.
东东进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列-1,2,3的最佳值为![]() ;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列-4,-3,1的最佳值为
(2)将“-4,-3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将2,-9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的最佳值为1,求a的值.
参考答案:
【答案】(1)3;(2)![]() ;-3,2,-4或2,-3,-4.(3)a=11或4或10.
;-3,2,-4或2,-3,-4.(3)a=11或4或10.
【解析】
(1)根据上述材料给出的方法计算其相应的最佳值为即可;
(2)按照三个数不同的顺序排列算出最佳值,由计算可以看出,要求得这些数列的最佳值的最小值;只有当前两个数的和的绝对值最小,最小只能为|3+2|=1,由此得出答案即可;
(3)分情况算出对应的数值,建立方程求得a的数值即可.
(1)因为|4|=4,![]() =3.5,
=3.5,![]() =3,
=3,
所以数列4,3,1的最佳值为3.
故答案为:3;
(2)对于数列4,3,2,因为|4|=4,![]() =
=![]() ,
,![]() =
=![]() ,
,
所以数列4,3,2的最佳值为![]() ;
;
对于数列4,2,3,因为|4|=4,![]() =1,
=1,![]() =
=![]() ,
,
所以数列4,2,3的最佳值为1;
对于数列2,4,3,因为|2|=2,![]() =1,
=1,![]() =
=![]() ,
,
所以数列2,4,3的最佳值为1;
对于数列2,3,4,因为|2|=2,![]() =
=![]() ,
,![]() =
=![]() ,
,
所以数列2,3,4的最佳值为![]()
∴数列的最佳值的最小值为![]() =
=![]() ,
,
数列可以为:3,2,4或2,3,4.
故答案为:![]() ,3,2,4或2,3,4.
,3,2,4或2,3,4.
(3)当![]() =1,则a=0或4,不合题意;
=1,则a=0或4,不合题意;
当![]() =1,则a=11或7;
=1,则a=11或7;
当a=7时,数列为9,7,2,因为|9|=9,![]() =1,
=1,![]() =0,
=0,
所以数列2,3,4的最佳值为0,不符合题意;
当![]() =1,则a=4或10.
=1,则a=4或10.
∴a=11或4或10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂一周计划每日生产某产品100吨,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为“+”,减少的吨数记为“﹣”)
星期
一
二
三
四
五
六
日
增减/吨
﹣1
+3
﹣2
+4
+7
﹣7
﹣11
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t)
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你估计总体小王所居住的小区中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列举法(画树状图或列表)求抽取出的2个家庭来自不同范围的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在数轴上
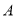 点表示数
点表示数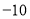 ,
,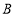 点表示数6,
点表示数6,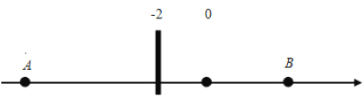
(1)A、B两点之间的距离等于_________;
(2)在数轴上有一个动点
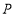 ,它表示的数是
,它表示的数是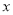 ,则
,则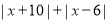 的最小值是_________;
的最小值是_________;(3)若点
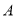 与点
与点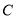 之间的距离表示为
之间的距离表示为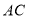 ,点
,点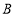 与点
与点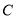 之间的距离表示为
之间的距离表示为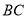 ,请在数轴上找一点
,请在数轴上找一点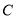 ,使
,使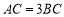 ,则
,则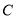 点表示的数是_________;
点表示的数是_________;(4)若在原点
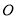 的左边2个单位处放一挡板,一小球甲从点
的左边2个单位处放一挡板,一小球甲从点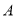 处以5个单位/秒的速度向右运动;同时另一小球乙从点
处以5个单位/秒的速度向右运动;同时另一小球乙从点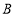 处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为
处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为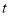 秒,请用
秒,请用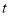 来表示甲、乙两小球之间的距离
来表示甲、乙两小球之间的距离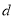 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元,设小明快递物品x千克.
(1)根据题意,填写下表:
快递物品重量(千克)
0.5
1
3
4
…
甲公司收费(元)
22
…
乙公司收费(元)
11
51
67
…
(2)设甲快递公司收费y1元,乙快递公司收费y2元,分别写出y1,y2关于x的函数关系式;
(3)当x>3时,小明应选择哪家快递公司更省钱?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种水果的价格如表:
购买的质量(千克)
不超过10千克
超过10千克
每千克价格
6元
5元
张欣两次共购买了25千克这种水果(第二次多于第一次),共付款132元.问张欣第一次、第二次分别购买了多少千克这种水果?
-
科目: 来源: 题型:
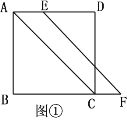
查看答案和解析>>【题目】已知,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,且AE=CF,连接AC,EF.
(1)如图①,求证:EF//AC;
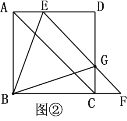
(2)如图②,EF与边CD交于点G,连接BG,BE,
①求证:△BAE≌△BCG;
②若BE=EG=4,求△BAE的面积.
相关试题

