【题目】某电子厂生产一种新型电子产品,每件制造成本为20元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月获得的利润为400万元?
(3)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过520万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
参考答案:
【答案】(1)z=﹣2x2+140x﹣2000;(2)30元或40元;(3)当销售单价为37元时,厂商每月获得的利润最大,最大利润为442万元.
【解析】试题分析:(1)根据每月的利润z=(x-18)y,再把y=-2x+100代入即可求出z与x之间的函数解析式,
(2)把z=440代入z=-2x2+136x-1800,解这个方程即可;
(3)根据厂商每月的制造成本不超过520万元,以及成本价20元,得出销售单价的取值范围,进而得出最大利润.
试题解析:(1)z=(x﹣20)y=(x﹣20)(﹣2x+100)=﹣2x2+140x﹣2000,
故z与x之间的函数解析式为z=﹣2x2+140x﹣2000;
(2)由z=400,得400=﹣2x2+140x﹣2000,
解这个方程得x1=30,x2=40
所以销售单价定为30元或40元;
(3)∵厂商每月的制造成本不超过520万元,每件制造成本为20元,
∴每月的生产量小于等于![]() =26万件,
=26万件,
由y=﹣2x+100≤26,得:x≥37,
又由限价40元,得37≤x≤40,
∵z=﹣2x2+140x﹣2000=﹣2(x﹣35)2+450,
∴图象开口向下,对称轴右侧z随x的增大而减小,
∴当x=37时,z最大为442万元.
当销售单价为37元时,厂商每月获得的利润最大,
最大利润为442万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC的边AB绕着点A顺时针旋转
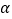 (
(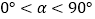 )得到AB′,边AC绕着点A逆时针旋转
)得到AB′,边AC绕着点A逆时针旋转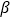 (
(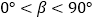 )得到AC′,联结B′C′,当
)得到AC′,联结B′C′,当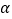 +
+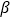 =60°时,我们称
=60°时,我们称 AB′C′是
AB′C′是 ABC的“双旋三角形”,如果等边
ABC的“双旋三角形”,如果等边 ABC的边长为a, 那么它所得的“双旋三角形”中B′C′=___________(用含a的代数式表示).
ABC的边长为a, 那么它所得的“双旋三角形”中B′C′=___________(用含a的代数式表示).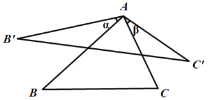
-
科目: 来源: 题型:
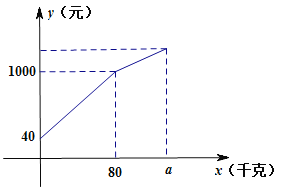
查看答案和解析>>【题目】一果农带了若干千克自产的苹果进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又半价售完剩下的苹果.售出苹果千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)果农自带的零钱是多少?
(2)降价前他每千克苹果出售的价格是多少?
(3)降价售完剩余苹果后,这时他手中的钱(含备用零钱)是1120元,问果农一共带了多少千克苹果?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
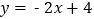 的图像与
的图像与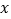 轴、
轴、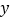 轴分别交于点B、A.以AB为边在第一象限内作等腰直角三角形ABC,且∠ABC=90°,BA=BC,作OB的垂直平分线l,交直线AB与点E,交x轴于点G.
轴分别交于点B、A.以AB为边在第一象限内作等腰直角三角形ABC,且∠ABC=90°,BA=BC,作OB的垂直平分线l,交直线AB与点E,交x轴于点G.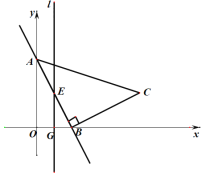
(1)求点
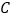 的坐标;
的坐标;(2)在OB的垂直平分线l上有一点M,且点M与点C位于直线AB的同侧,使得
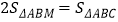 ,求点M的坐标;
,求点M的坐标;(3)在(2)的条件下,联结CE、CM,判断△CEM的形状,并给予证明;
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面上,Rt△ABC与直径为CE的半圆O如图1摆放,∠B=90°,AC=2CE=m,BC=n,半圆O交BC边于点D,将半圆O绕点C按逆时针方向旋转,点D随半圆O旋转且∠ECD始终等于∠ACB,旋转角记为α(0°≤α≤180°)
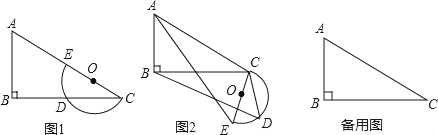
(1)当α=0°时,连接DE,则∠CDE= °,CD= ;
(2)试判断:旋转过程中
 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;(3)若m=10,n=8,当α=∠ACB时,求线段BD的长;
(4)若m=6,n=4
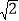 ,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长.
,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(-2,0),B(0,1).
(1)点C的坐标是 ;
(2)将△ABC沿x轴正方向平移得到△A′ B′C′,且B,C两点的对应点B′,C′恰好落在反比例函数
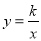 的图象上,求该反比例函数的解析式.
的图象上,求该反比例函数的解析式.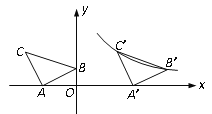
相关试题

