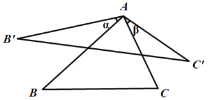
【题目】如图,将△ABC的边AB绕着点A顺时针旋转![]() (
(![]() )得到AB′,边AC绕着点A逆时针旋转
)得到AB′,边AC绕着点A逆时针旋转![]() (
(![]() )得到AC′,联结B′C′,当
)得到AC′,联结B′C′,当![]() +
+![]() =60°时,我们称
=60°时,我们称![]() AB′C′是
AB′C′是![]() ABC的“双旋三角形”,如果等边
ABC的“双旋三角形”,如果等边![]() ABC的边长为a, 那么它所得的“双旋三角形”中B′C′=___________(用含a的代数式表示).
ABC的边长为a, 那么它所得的“双旋三角形”中B′C′=___________(用含a的代数式表示).
参考答案:
【答案】![]()
【解析】
作AD⊥B′C′于点D,根据题意与旋转和等边三角形的的性质可得,△AB′C′是顶角为120°的等腰三角形,再根据等腰三角形的性质可得∠DA B′=60°,B′C′=2 B′D,根据sin∠DA B′=![]() 即可得解.
即可得解.
解:作AD⊥B′C′于点D,
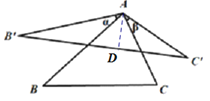
∵△ABC为等边三角形,![]() +
+![]() =60°,
=60°,
∴AB′=AC′,∠B′AC′=120°,
∴∠B′=30°,∴B′D=![]() a,
a,
则B′C′=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边 ABC 的边长是 2 , D 、 E 分别为 AB 、 AC 的中点,连接CD ,过 E 点作 EF // DC 交 BC 的延长线于点 F
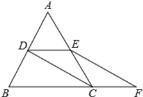
(1) 求证:四边形 CDEF 是平行四边形;
(2)求四边形 CDEF 的周长
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
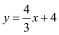 分别交
分别交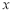 轴,
轴,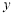 轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.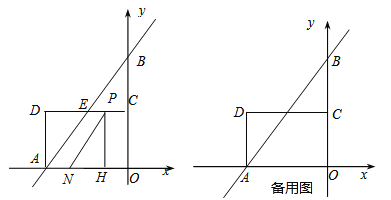
(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作
 ,垂足为H,连接NP.设点P的运动时间为
,垂足为H,连接NP.设点P的运动时间为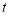 秒.
秒.①若△NPH的面积为1,求
 的值;
的值;②点Q是点B关于点A的对称点,问
 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.

-
科目: 来源: 题型:
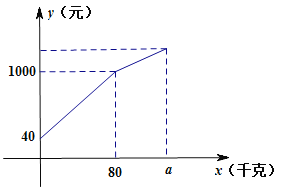
查看答案和解析>>【题目】一果农带了若干千克自产的苹果进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又半价售完剩下的苹果.售出苹果千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)果农自带的零钱是多少?
(2)降价前他每千克苹果出售的价格是多少?
(3)降价售完剩余苹果后,这时他手中的钱(含备用零钱)是1120元,问果农一共带了多少千克苹果?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电子厂生产一种新型电子产品,每件制造成本为20元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月获得的利润为400万元?
(3)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过520万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
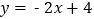 的图像与
的图像与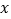 轴、
轴、 轴分别交于点B、A.以AB为边在第一象限内作等腰直角三角形ABC,且∠ABC=90°,BA=BC,作OB的垂直平分线l,交直线AB与点E,交x轴于点G.
轴分别交于点B、A.以AB为边在第一象限内作等腰直角三角形ABC,且∠ABC=90°,BA=BC,作OB的垂直平分线l,交直线AB与点E,交x轴于点G.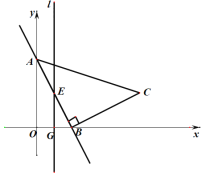
(1)求点
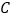 的坐标;
的坐标;(2)在OB的垂直平分线l上有一点M,且点M与点C位于直线AB的同侧,使得
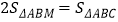 ,求点M的坐标;
,求点M的坐标;(3)在(2)的条件下,联结CE、CM,判断△CEM的形状,并给予证明;
相关试题

