【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A( ![]() ,0),B(0,2),则点B2016的坐标为 .
,0),B(0,2),则点B2016的坐标为 . 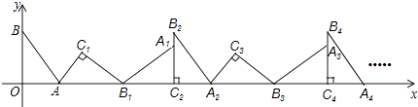
参考答案:
【答案】(6048,2)
【解析】解:∵AO= ![]() ,BO=2,
,BO=2,
∴AB= ![]() =
= ![]() ,
,
∴OA+AB1+B1C2=6,
∴B2的横坐标为:6,且B2C2=2,
∴B4的横坐标为:2×6=12,
∴点B2016的横坐标为:2016÷2×6=6048.
∴点B2016的纵坐标为:2.
∴点B2016的坐标为:(6048,2).
故答案为:(6048,2).
首先根据已知求出三角形三边长度,然后通过旋转发现,B、B2、B4…,即可得每偶数之间的B相差6个单位长度,根据这个规律可以求得B2016的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b和反比例函数y=
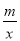 的图象的两个交点.
的图象的两个交点.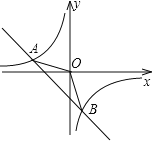
(1)求一次函数和反比例函数的解析式;
(2)观察图象,直接写出不等式kx+b﹣
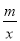 <0的解集.
<0的解集.(3)P是x轴上的一点,且满足△APB的面积是9,写出P点的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的10
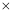 5(行
5(行 列)的数阵,是由一些连续奇数组成的,形如图框中的四个数,设第一行的第一个数为
列)的数阵,是由一些连续奇数组成的,形如图框中的四个数,设第一行的第一个数为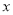 .
.(1)用含
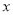 的式子表示另外三个数;
的式子表示另外三个数;(2)若这样框中的四个数的和是200,求出这四个数;
(3)是否存在这样的四个数,它们的和为246?为什么?
【答案】(1)x+2,x+8,x+10;(2)45,47,53,55;(3)不存在.
【解析】试题分析:(1)观察图框中的四个数,根据这四个数之间的数量关系,直接写出答案即可;(2)根据框中的四个数的和是200,列出方程,解方程即可;(3)根据框中的四个数的和是246,列出方程,解方程,根据方程解得情况判断是否存在即可.
试题解析:
(1)
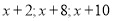 .
.(2)根据题意得:
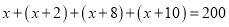 ,
,解之得,
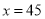 .
.∴x+2=47,x+8=53,x+10=55.
答:这四个数分别为45、47、53、55.
(3)不存在.
由
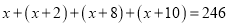 .
.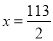 .
.而奇数是整数,所以不存在满足条件的数.
【题型】解答题
【结束】
25【题目】某单位计划购买电脑若干台,经了解同一型号市场预售价均为每台5000元.现有两商场优惠促销,甲商场:购买不超过2台按原价销售,超过2台的部分每台打7折;乙商场:每台均打8折.
(1)若学校购买5台,哪家商场较优惠?购买7台呢?
(2)买多少台时两商场所需费用一样多?
(3)你知道学校怎样选购更省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知C,D,E三点在直线AB上,P为直线AB外一点,PC=1,PD=2,PE=3,则点P到直线AB的距离( )
A. 小于1B. 不小于1C. 大于1D. 不大于1
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各式:
(1) +(
+(  )﹣2+(π﹣1)0
)﹣2+(π﹣1)0
(2)(3﹣π)0+4×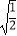 ﹣
﹣ 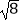 +|1﹣
+|1﹣ 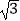 |.
|. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积. 某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
作AD⊥BC于D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x→利用勾股定理求出AD的长,再计算三角形的面积.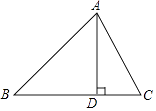
-
科目: 来源: 题型:
查看答案和解析>>【题目】某创业团队有研发、管理和操作三个小组,各组的日工资和人数如下表:
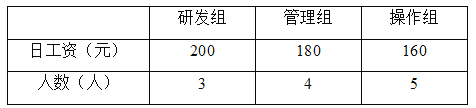
现从管理组分别抽调1人到研发组和操作组,调整后与调整前相比,下列说法中正确的有( )
①平均日工资增大 ②日工资的方差减小
③日工资的中位数不变 ④日工资的众数不变
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

