搜索
【题目】如图，等腰△ABC中，AB=AC=8，BC=5，AB的垂直平分线DE交AB于点D，交AC于点E，则△BEC的周长为（ ） 
A.13
B.14
C.15
D.16
参考答案：
【答案】A
【解析】解：∵DE是AB的垂直平分线，
∴AE=BE，
∴△BEC周长=BE+CE+BC=AE+CE+BC=AC+BC，
∵腰长AB=8，
∴AC=AB=8，
∴△BEC周长=8+5=13．
故选A．
【考点精析】通过灵活运用线段垂直平分线的性质和等腰三角形的性质，掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等；等腰三角形的两个底角相等（简称：等边对等角）即可以解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，△ABC的三个顶点的位置如图所示，现将△ABC沿AA′的方向平移，使得点A移至图中的点A′的位置．
(1)在直角坐标系中，画出平移后所得△A′B′C′(其中B′、C′分别是B、C的对应点)；
(2)求△ABC的面积；
(3)以A、B、C、D为顶点构造平行四边形，则D点坐标为____________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=
x2+bx﹣2与x轴交于A、B两点，与y轴交于C点，且A（﹣1，0）．
（1）求抛物线的解析式及顶点D的坐标；
（2）判断△ABC的形状，证明你的结论；
（3）点M是x轴上的一个动点，当△DCM的周长最小时，求点M的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，在平面直角坐标中，边长为2的正方形OABC的两顶点A，C分别在y轴、x轴的正半轴上，O为坐标原点．现将正方形OABC绕O点顺时针旋转，当A点第一次落在直线y=x上时停止旋转，旋转过程中，AB边交直线y=x于点M，BC边交x轴于点N．
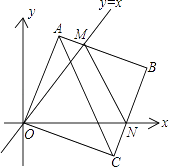
（1）当A点第一次落在直线y=x上时，求点A所经过的路线长；
（2）在旋转过程中，当MN和AC平行时，求正方形OABC旋转的度数；
（3）设△MBN的周长为p，在旋转正方形OABC的过程中，p值是否有变化？请证明你的结论． -
科目： 来源： 题型：
查看答案和解析>>【题目】青山化工厂与A、B两地有公路、铁路相连，这家工厂从A地购买一批每吨1000元的原料经铁路120km和公路10km运回工厂，制成每吨8000元的产品经铁路110km和公路20km销售到B地．已知铁路的运价为1.2元/（吨·千米)，公路的运价为1.5元/(吨·千米)，且这两次运输共支出铁路运费124800元，公路运费19500元．
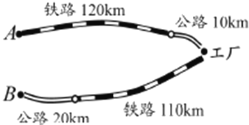
（1）设原料重x吨，产品重y吨，根据题中数量关系填写下表
原料x吨
产品y吨
合计（元）
铁路运费
124800
公路运费
19500
根据上表列方程组求原料和产品的重量．
（2）这批产品的销售款比原料费与运输费的和多多少元?
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题中，真命题是( )
A. 如果三角形三个角的度数比是3：4：5，那么这个三角形是直角三角形
B. 如果直角三角形两直角边的长分别为a和b，那么斜边的长为a2+b2
C. 若三角形三边长的比为1：2：3，则这个三角形是直角三角形
D. 如果直角三角形两直角边分别为a和b，斜边为c，那么斜边上的高h的长为
-
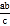
科目： 来源： 题型：
查看答案和解析>>【题目】在同一条道路上，甲车从A地到B地，乙车从B地到A地，乙先出发，图中的折线段表示甲、乙两车之间的距离y（千米）与行驶时间x（小时）的函数关系的图象，下列说法错误的是（ ）
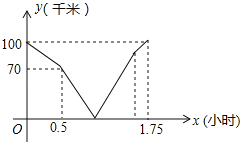
A. 乙先出发的时间为0.5小时 B. 甲的速度是80千米/小时
C. 甲出发0.5小时后两车相遇 D. 甲到B地比乙到A地早
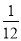小时
相关试题
