【题目】在四边形ABCD中,AD∥BC,点E在BC边的延长线上,CE=BC,连接AE,交CD边于点F,且CF=DF. 
(1)如图1,求证:AD=BC;
(2)如图2,连接BD、DE,若BD⊥DE,请判定四边形ABCD的形状,并证明.
参考答案:
【答案】
(1)证明:∵AD∥BC,
∴∠D=∠ECF,
在△ADF和△ECF中, 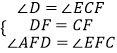 ,
,
∴△ADF≌△ECF(ASA),
∴AD=CE,
∵CE=BC,
∴AD=BC
(2)解:四边形ABCD是菱形;理由如下:
∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,
∵BD⊥DE,
∴∠BDE=90°,
∵CE=BC,
∴CD= ![]() BE=BC,
BE=BC,
∴四边形ABCD是菱形
【解析】(1)由平行线的性质得出∠D=∠ECF,由ASA证明△ADF≌△ECF,得出AD=CE,即可得出结论;(2)首先四边形ABCD是平行四边形,由直角三角形斜边上的中线性质得出CD= ![]() BE=BC,即可得出四边形ABCD是菱形.
BE=BC,即可得出四边形ABCD是菱形.
【考点精析】利用平行线的性质对题目进行判断即可得到答案,需要熟知两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B、C、D、E五位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)若已确定A打第一场,再从其余四位同学中随机选取一位,求恰好选中B同学的概率;
(2)请用画树状图或列表法,求恰好选中A、B两位同学的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知有理数a、b在数轴上的对应点如图所示.
(1)已知a=–2.3,b=0.4,计算|a+b|–|a|–|1–b|的值;
(2)已知有理数a、b,计算|a+b|–|a|–|1–b|的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下面系列图形中第一个最小的等腰直角三角形的面积都是 1,后一个等腰直角三 角形的斜边恰好是前一个等腰直角三角形的直角边的 2 倍,请计算每个图形的面积,并填在 相应的空中,

图形 1 面积=_____,图形 2 面积=_____,图形 3 的面积=_____,
 …………
…………图形 4 的面积=_____, 图形 n 的面积=_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是安装在斜屋面上的热水器,图2是安装该热水器的侧面示意图.已知,斜屋面的倾角为25°,长为2.1米的真空管AB与水平线AD的夹角为40°,安装热水器的铁架水平横管BC长0.2米,求铁架垂直管CE的长(结果精确到0.01米).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,平面直角坐标系xOy中,四边形OABC是矩形,点A,C的坐标分别为(6,0),(0,2).点D是线段BC上的一个动点(点D与点B,C不重合),过点D作直线y=-
 x+b交折线O-A-B于点E.
x+b交折线O-A-B于点E.(1)在点D运动的过程中,若△ODE的面积为S,求S与b的函数关系式,并写出自变量的取值范围;
(2)如图2,当点E在线段OA上时,矩形OABC关于直线DE对称的图形为矩形O′A′B′C′,C′B′分别交CB,OA于点D,M,O′A′分别交CB,OA于点N,E.求证:四边形DMEN是菱形;
(3)问题(2)中的四边形DMEN中,ME的长为____________.


-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料并填空: 在体育比赛中,我们常常会遇到计算比赛场次的问题,这时我们可以借助数线段的方法来计算.比如在一个小组中有 4 个队,进行单循环比赛,我们要计算总的比赛场次,我们就 设这四个队分别为 A、B、C、D,并把它们标在同一条线段上,如下图:
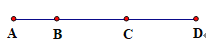
因为单循环比赛就是每两个队之间都要比赛一场,这就相当于,在上述图形中四个点连接线段,按一定规律得到的线段有:
AB,AC,AD…………3 条
BC,BD………………2 条
CD……………………1 条
总的线段条数是 3+2+1=6
所以可知 4 个队进行单循环比赛共比赛六场.
(1).类比上述想法,若一个小组有 6 个队,进行单循环比赛,则总的比赛场次是_____
(2).类比上述想法,若一个小组有 n 个队,进行单循环比赛,则总的比赛场次是_____
(3).我们知道 2006 年世界杯共有 32 支代表队参加比赛,共分成 8 个小组,每组 4 个 代表队.第一阶段每个小组进行单循环比赛.则第一阶段共 需 要 进 行_______ 场比赛.
(4).若分成 m 个小组,每个小组有 n 个队,第一阶段每个小组进行单循环比赛.则第 一阶段共需要进行_____________场比赛.
相关试题

