【题目】在一条笔直的公路上有![]() 、
、![]() 两地,甲骑自行车从
两地,甲骑自行车从![]() 地到
地到![]() 地;乙骑自行车从
地;乙骑自行车从![]() 地到
地到![]() 地,到达
地,到达![]() 地后立即按原路返回,如图是甲乙两人离
地后立即按原路返回,如图是甲乙两人离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数图像,根据图像解答以下问题:
之间的函数图像,根据图像解答以下问题:
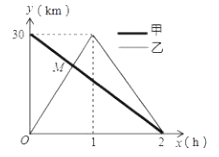
(1)求出甲离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数表达式;
之间的函数表达式;
(2)求出点![]() 的坐标,并解释改点坐标所表示的实际意义;
的坐标,并解释改点坐标所表示的实际意义;
(3)若两人之间保持的距离不超过![]() 时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持练习时
时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持练习时![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() ;(2) 点M的坐标是(
;(2) 点M的坐标是(![]() ,20),点M的坐标表示:甲、乙经过
,20),点M的坐标表示:甲、乙经过![]() h第一次相遇,此时离点B的距离是20km;(3)
h第一次相遇,此时离点B的距离是20km;(3) ![]() 当或
当或![]() ≤x≤2.
≤x≤2.
【解析】
(1) 根据函数图象就可以得出A, C点坐标,用待定系数法可得甲离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数表达式;
之间的函数表达式;
(2) 根据函数图象求出OC的解析式,求出OC与AB的交点可得M点坐标, 根据图像可得M的坐标表示的含义;
(3) 分情况讨论,当![]() -
-![]() ≤3,
≤3,![]() -
-![]() ≤3,分别求出x的值可以得出结论.
≤3,分别求出x的值可以得出结论.
解:如图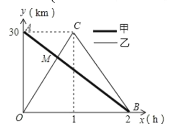
可得甲离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数表达式即为AC的函数表达式,
之间的函数表达式即为AC的函数表达式,
其经过点A(0,30),B(2,0),
设其表达式为:![]() ,可得
,可得![]() ,
,
解得:![]() ,
,
甲离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数表达式为:
之间的函数表达式为:![]() .
.
(2) 设OC的解析式为![]() ,其经过点C(1,30),
,其经过点C(1,30),
可得![]() =30,
=30,![]()
![]() ;
;
设BC的解析式为![]() ,其经过点C(1,30),B(2,0),
,其经过点C(1,30),B(2,0),
可得:![]() ,解得
,解得![]() ,
,
![]()
![]()
![]()
![]()
可得M点为AB与OC的交点,![]() =
=![]() 可得-15x+30=30x,
可得-15x+30=30x,
解得:x=![]() ,
,![]()
![]() =
=![]() =20,
=20,
![]() 点M的坐标是(
点M的坐标是(![]() ,20),点M的坐标表示:甲、乙经过
,20),点M的坐标表示:甲、乙经过![]() h第一次相遇,此时离点B的距离是20km;
h第一次相遇,此时离点B的距离是20km;
(3)分情况讨论:
①![]() -
-![]() ≤3,
≤3,![]() -
-![]() ≤3时
≤3时
![]() 解得:
解得:![]()
②(-30x+60)-(15x+30)≤3
解得:x≥![]()
![]()
![]() ≤x≤2
≤x≤2
综上所述:![]() 当或
当或![]() ≤x≤2两人能够用无线对讲机保持联系.
≤x≤2两人能够用无线对讲机保持联系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称
单价(元)
数量(个)
金额(元)
挂钟
30
2
60
垃圾桶
15
塑料鞋架
40
艺术饰品
a
2
90
电热水壶
35
1
b
合计
8
280
(1)直接写出a= ,b= ;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术饰品和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H,将△ADF绕点A顺时针旋转90°得到△ABG,若BE=2,DF=3,则AH的长为 .
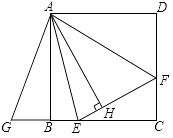
-
科目: 来源: 题型:
查看答案和解析>>【题目】如(图1),在平面直角坐标系中,
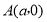 ,
,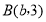 ,
,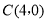 ,且满足
,且满足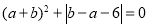 ,线段
,线段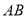 交
交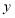 轴于
轴于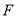 点.
点.(1)填空:
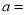 ,
,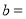 ;
;(2)点
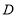 为
为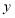 轴正半轴上一点,若
轴正半轴上一点,若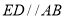 ,
,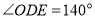 ,且
,且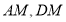 分别平分
分别平分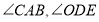 ,如(图2),求
,如(图2),求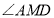 的度数;
的度数;(3)求点
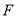 的坐标;
的坐标;(4)如(图3),在
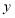 轴上是否存在一点
轴上是否存在一点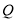 ,使三角形
,使三角形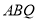 的面积和三角形
的面积和三角形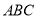 的面积相等?若存在,求出
的面积相等?若存在,求出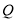 点坐标,若不存在,说明理由.
点坐标,若不存在,说明理由.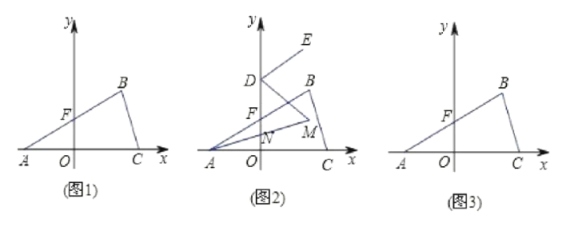
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若关于
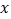 、
、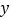 的二元一次方程组
的二元一次方程组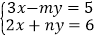 的解是
的解是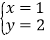 ,求关于
,求关于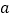 、
、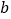 的二元一次方程组
的二元一次方程组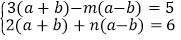 的解.
的解.(2)如图,点
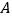 、
、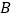 的坐标分别是
的坐标分别是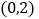 、
、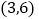 ,点
,点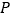 为
为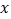 轴上的一个动点,若点
轴上的一个动点,若点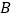 关于直线
关于直线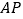 的对称点
的对称点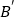 恰好落在
恰好落在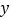 轴上,写出点
轴上,写出点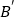 的坐标.
的坐标.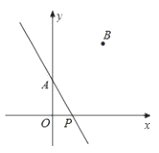
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
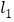 的解析式为
的解析式为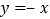 ,直线
,直线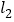 与
与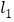 交于点
交于点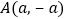 ,与
,与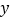 轴交于点
轴交于点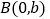 ,其中
,其中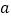 ,
,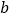 满足
满足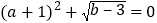 .
.(1)求直线
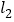 的解析式;
的解析式;(2)在平面直角坐标系中有一点
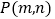 ,若
,若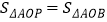 ,则
,则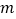 与
与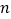 满足的关系式是什么?
满足的关系式是什么?(3)已知平行于
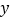 轴且位于
轴且位于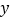 轴左侧有一动直线,分别与
轴左侧有一动直线,分别与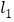 ,
,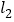 交于点
交于点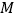 ,
,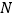 且点
且点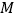 在点
在点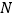 的下方,点
的下方,点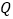 为
为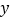 轴上一动点,且
轴上一动点,且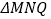 为等腰直角三角形,请直接写出满足条件的点
为等腰直角三角形,请直接写出满足条件的点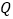 的坐标.
的坐标.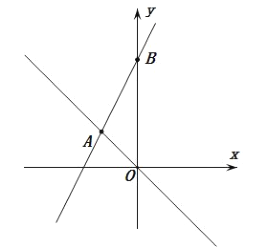
-
科目: 来源: 题型:
查看答案和解析>>【题目】英国《
 ?》杂志最近对30部手机进行了检测,结果发现有近四分之一的手机携带的细菌数量达到可接受数量的10倍,其中一部最脏的手机一度让它的主人出现严重消化不良.在手机上发现的有害细菌中,最为常见的有害细菌当属金黄色葡萄球菌.这种细菌可导致一系列感染,金黄色葡萄球菌为球形,直径
?》杂志最近对30部手机进行了检测,结果发现有近四分之一的手机携带的细菌数量达到可接受数量的10倍,其中一部最脏的手机一度让它的主人出现严重消化不良.在手机上发现的有害细菌中,最为常见的有害细菌当属金黄色葡萄球菌.这种细菌可导致一系列感染,金黄色葡萄球菌为球形,直径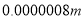 左右,0.0000008米这个数用科学记数法表示为( )
左右,0.0000008米这个数用科学记数法表示为( )A.
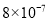 米B.
米B.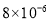 米C.
米C.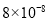 米D.
米D.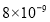 米
米
相关试题

