【题目】如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H,将△ADF绕点A顺时针旋转90°得到△ABG,若BE=2,DF=3,则AH的长为 . 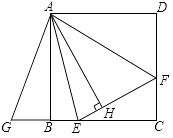
参考答案:
【答案】6
【解析】解:由旋转的性质可知:AF=AG,∠DAF=∠BAG.
∵四边形ABCD为正方形,
∴∠BAD=90°.
又∵∠EAF=45°,
∴∠BAE+∠DAF=45°.
∴∠BAG+∠BAE=45°.
∴∠GAE=∠FAE.
在△GAE和△FAE中 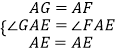 ,
,
∴△GAE≌△FAE.
∵AB⊥GE,AH⊥EF,
∴AB=AH,GE=EF=5.
设正方形的边长为x,则EC=x﹣2,FC=x﹣3.
在Rt△EFC中,由勾股定理得:EF2=FC2+EC2,即(x﹣2)2+(x﹣3)2=25.
解得:x=6.
∴AB=6.
∴AH=6.
所以答案是:6.
【考点精析】本题主要考查了正方形的性质和旋转的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,
 时注满水槽,水槽内水面的高度
时注满水槽,水槽内水面的高度 与注水时间
与注水时间 之间的函数图像如图2所示.如果将正方体铁块取出,又经过____秒恰好将水槽注满.
之间的函数图像如图2所示.如果将正方体铁块取出,又经过____秒恰好将水槽注满.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图所示,下列结论:①abc<0;②2a+b<0;③b2﹣4ac=0;④8a+c<0;⑤a:b:c=﹣1:2:3,其中正确的结论有 .
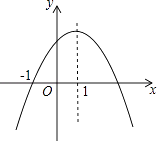
-
科目: 来源: 题型:
查看答案和解析>>【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称
单价(元)
数量(个)
金额(元)
挂钟
30
2
60
垃圾桶
15
塑料鞋架
40
艺术饰品
a
2
90
电热水壶
35
1
b
合计
8
280
(1)直接写出a= ,b= ;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术饰品和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如(图1),在平面直角坐标系中,
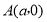 ,
,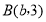 ,
,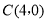 ,且满足
,且满足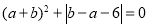 ,线段
,线段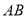 交
交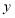 轴于
轴于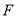 点.
点.(1)填空:
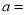 ,
,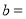 ;
;(2)点
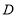 为
为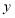 轴正半轴上一点,若
轴正半轴上一点,若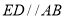 ,
,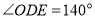 ,且
,且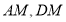 分别平分
分别平分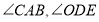 ,如(图2),求
,如(图2),求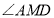 的度数;
的度数;(3)求点
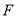 的坐标;
的坐标;(4)如(图3),在
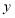 轴上是否存在一点
轴上是否存在一点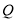 ,使三角形
,使三角形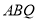 的面积和三角形
的面积和三角形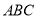 的面积相等?若存在,求出
的面积相等?若存在,求出 点坐标,若不存在,说明理由.
点坐标,若不存在,说明理由.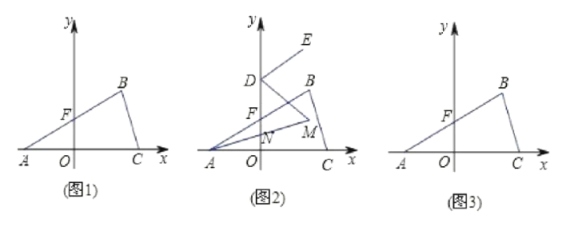
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的公路上有
 、
、 两地,甲骑自行车从
两地,甲骑自行车从 地到
地到 地;乙骑自行车从
地;乙骑自行车从 地到
地到 地,到达
地,到达 地后立即按原路返回,如图是甲乙两人离
地后立即按原路返回,如图是甲乙两人离 地的距离
地的距离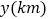 与行驶时间
与行驶时间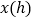 之间的函数图像,根据图像解答以下问题:
之间的函数图像,根据图像解答以下问题: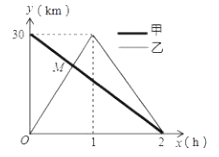
(1)求出甲离
 地的距离
地的距离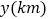 与行驶时间
与行驶时间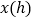 之间的函数表达式;
之间的函数表达式;(2)求出点
 的坐标,并解释改点坐标所表示的实际意义;
的坐标,并解释改点坐标所表示的实际意义;(3)若两人之间保持的距离不超过
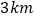 时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持练习时
时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持练习时 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若关于
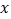 、
、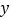 的二元一次方程组
的二元一次方程组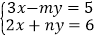 的解是
的解是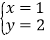 ,求关于
,求关于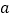 、
、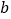 的二元一次方程组
的二元一次方程组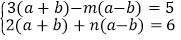 的解.
的解.(2)如图,点
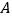 、
、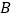 的坐标分别是
的坐标分别是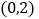 、
、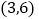 ,点
,点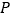 为
为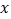 轴上的一个动点,若点
轴上的一个动点,若点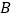 关于直线
关于直线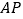 的对称点
的对称点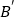 恰好落在
恰好落在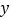 轴上,写出点
轴上,写出点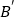 的坐标.
的坐标.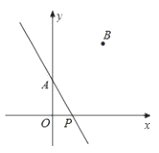
相关试题

