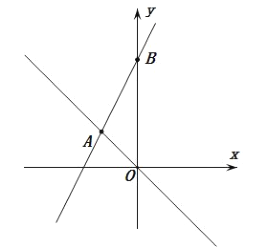
【题目】如图,在平面直角坐标系中,直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其中
,其中![]() ,
,![]() 满足
满足![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)在平面直角坐标系中有一点![]() ,若
,若![]() ,则
,则![]() 与
与![]() 满足的关系式是什么?
满足的关系式是什么?
(3)已知平行于![]() 轴且位于
轴且位于![]() 轴左侧有一动直线,分别与
轴左侧有一动直线,分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() 且点
且点![]() 在点
在点![]() 的下方,点
的下方,点![]() 为
为![]() 轴上一动点,且
轴上一动点,且![]() 为等腰直角三角形,请直接写出满足条件的点
为等腰直角三角形,请直接写出满足条件的点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)![]() 的解析式为
的解析式为![]() ;(2) m+n=3或m+n=-3;(3)
;(2) m+n=3或m+n=-3;(3) ![]() (0,
(0,![]() ),
),![]() (0,
(0,![]() ),
),![]() (0,
(0,![]() ).
).
【解析】
(1)可得A(-1,1)B(0,3),设![]() 的解析式为
的解析式为![]() ,代入A(-1,1),可得
,代入A(-1,1),可得![]() 的解析式;
的解析式;
(2)①当点P在![]() 的右侧时,设点P为
的右侧时,设点P为![]() ,且
,且![]() B//
B//![]() ,
,![]() B的解析式为:y=-x+3,即:n=-m+3,m+n=3,②当点P
B的解析式为:y=-x+3,即:n=-m+3,m+n=3,②当点P![]() 在的左侧时,设点P为
在的左侧时,设点P为![]() ,,,可得B点关于O点的对称点位
,,,可得B点关于O点的对称点位![]() (0,-3)点在
(0,-3)点在![]() ;
;![]() 上,且
上,且![]()
![]() //
//![]() ,
,![]()
![]() 的解析式为:y=-x-3,即:n=-m-3,m+n=-3;
的解析式为:y=-x-3,即:n=-m-3,m+n=-3;
(3)设动直线为x=t,由题可得-1<t<0,则M(t,-t),N(t,2t+3),MN=3t+3,
当NM⊥NQ且NM=NQ时,Q(0,2t+3),由3t+3=-t,t=-![]() ,可得Q的值,
,可得Q的值,
当MN⊥MQ且NM=MQ时,Q(0,-t),由3t+3=-t,t=-![]() ,可得Q的值,
,可得Q的值,
当QN⊥QM且QN=QM时,Q(0,![]() ),可得2t+3-(
),可得2t+3-(![]() )=-t,解得t=
)=-t,解得t=![]() ,可得Q的值.
,可得Q的值.
解:(1)由题可得: a=-1,b=3
则点A(-1,1)B(0,3)
设![]() 的解析式为
的解析式为![]() ,代入A(-1,1)得:1=-k+3,
,代入A(-1,1)得:1=-k+3,
解得:k=2,
![]()
![]() 的解析式为
的解析式为![]()
(2)![]() ,则点P到AO的距离与点B到AO的距离相等,且点P位于h两侧;
,则点P到AO的距离与点B到AO的距离相等,且点P位于h两侧;
①当点P在![]() 的右侧时,设点P为
的右侧时,设点P为![]() ,且
,且![]() B//
B//![]()
![]()
![]() B的解析式为:y=-x+3,即:n=-m+3,m+n=3
B的解析式为:y=-x+3,即:n=-m+3,m+n=3
②当点P![]() 在的左侧时,设点P为
在的左侧时,设点P为![]() ,,
,,
可得B点关于O点的对称点位![]() (0,-3)点在
(0,-3)点在![]() ;
;![]() 上,且
上,且![]()
![]() //
//![]() ,
,
![]()
![]()
![]() 的解析式为:y=-x-3,即:n=-m-3,m+n=-3;
的解析式为:y=-x-3,即:n=-m-3,m+n=-3;
综合:m+n=3或m+n=-3;
(3)设动直线为x=t,由题可得-1<t<0,
则M(t,-t),N(t,2t+3),MN=3t+3,
当NM⊥NQ且NM=NQ时,Q(0,2t+3),由3t+3=-t,t=-![]() ,此时
,此时![]() (0,
(0,![]() )
)
当MN⊥MQ且NM=MQ时,Q(0,-t),由3t+3=-t,t=-![]() ,此时
,此时![]() (0,
(0,![]() )
)
当QN⊥QM且QN=QM时,Q(0,![]() ),可得2t+3-(
),可得2t+3-(![]() )=-t,解得t=
)=-t,解得t=![]() ,此时
,此时![]() (0,
(0,![]() ),
),
综上![]() (0,
(0,![]() ),
),![]() (0,
(0,![]() ),
),![]() (0,
(0,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如(图1),在平面直角坐标系中,
 ,
, ,
, ,且满足
,且满足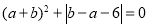 ,线段
,线段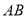 交
交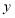 轴于
轴于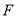 点.
点.(1)填空:
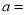 ,
,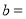 ;
;(2)点
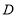 为
为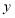 轴正半轴上一点,若
轴正半轴上一点,若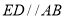 ,
,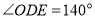 ,且
,且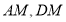 分别平分
分别平分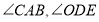 ,如(图2),求
,如(图2),求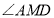 的度数;
的度数;(3)求点
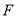 的坐标;
的坐标;(4)如(图3),在
 轴上是否存在一点
轴上是否存在一点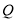 ,使三角形
,使三角形 的面积和三角形
的面积和三角形 的面积相等?若存在,求出
的面积相等?若存在,求出 点坐标,若不存在,说明理由.
点坐标,若不存在,说明理由.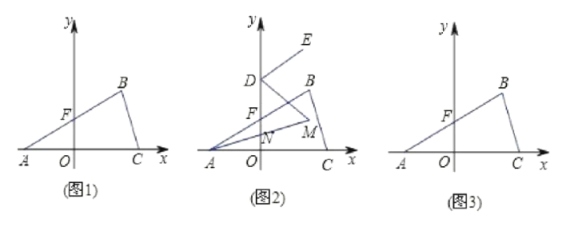
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的公路上有
 、
、 两地,甲骑自行车从
两地,甲骑自行车从 地到
地到 地;乙骑自行车从
地;乙骑自行车从 地到
地到 地,到达
地,到达 地后立即按原路返回,如图是甲乙两人离
地后立即按原路返回,如图是甲乙两人离 地的距离
地的距离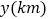 与行驶时间
与行驶时间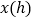 之间的函数图像,根据图像解答以下问题:
之间的函数图像,根据图像解答以下问题: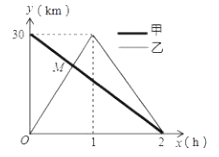
(1)求出甲离
 地的距离
地的距离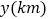 与行驶时间
与行驶时间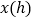 之间的函数表达式;
之间的函数表达式;(2)求出点
 的坐标,并解释改点坐标所表示的实际意义;
的坐标,并解释改点坐标所表示的实际意义;(3)若两人之间保持的距离不超过
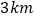 时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持练习时
时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持练习时 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若关于
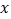 、
、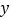 的二元一次方程组
的二元一次方程组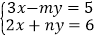 的解是
的解是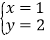 ,求关于
,求关于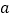 、
、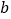 的二元一次方程组
的二元一次方程组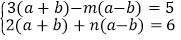 的解.
的解.(2)如图,点
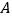 、
、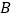 的坐标分别是
的坐标分别是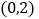 、
、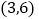 ,点
,点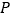 为
为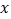 轴上的一个动点,若点
轴上的一个动点,若点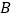 关于直线
关于直线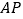 的对称点
的对称点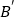 恰好落在
恰好落在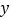 轴上,写出点
轴上,写出点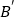 的坐标.
的坐标.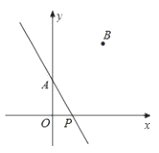
-
科目: 来源: 题型:
查看答案和解析>>【题目】英国《
 ?》杂志最近对30部手机进行了检测,结果发现有近四分之一的手机携带的细菌数量达到可接受数量的10倍,其中一部最脏的手机一度让它的主人出现严重消化不良.在手机上发现的有害细菌中,最为常见的有害细菌当属金黄色葡萄球菌.这种细菌可导致一系列感染,金黄色葡萄球菌为球形,直径
?》杂志最近对30部手机进行了检测,结果发现有近四分之一的手机携带的细菌数量达到可接受数量的10倍,其中一部最脏的手机一度让它的主人出现严重消化不良.在手机上发现的有害细菌中,最为常见的有害细菌当属金黄色葡萄球菌.这种细菌可导致一系列感染,金黄色葡萄球菌为球形,直径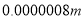 左右,0.0000008米这个数用科学记数法表示为( )
左右,0.0000008米这个数用科学记数法表示为( )A.
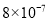 米B.
米B.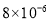 米C.
米C.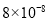 米D.
米D.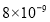 米
米 -
科目: 来源: 题型:
查看答案和解析>>【题目】在“植树节”期间,小王、小李两人想通过摸球的方式来决定谁去参加学校植树活动,规则如下:在两个盒子内分别装入标有数字1,2,3,4的四个和标有数字1,2,3的三个完全相同的小球,分别从两个盒子中各摸出一个球,如果所摸出的球上的数字之和小于6,那么小王去,否则就是小李去.
(1)用树状图或列表法求出小王去的概率;
(2)小李说:“这种规则不公平”,你认同他的说法吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某武警部队在一次地震抢险救灾行动中,探险队员在相距4米的水平地面A,B两处均探测出建筑物下方C处有生命迹象,已知在A处测得探测线与地面的夹角为30°,在B处测得探测线与地面的夹角为60°,求该生命迹象C处与地面的距离.(结果精确到0.1米,参考数据:
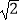 ≈1.41,
≈1.41, 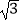 ≈1.73)
≈1.73)
相关试题

