【题目】给出以下命题:
①函数![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
②已知回归直线方程为![]() ,样本点的中心为
,样本点的中心为![]() ,则
,则![]() ;
;
③函数![]() 图象关于点
图象关于点![]() 对称且在
对称且在![]() 上单调递增;
上单调递增;
④根据党中央关于“精准”脱贫的要求,我州某农业经济部门决定派出五位相关专家对三个贫困地区进行调研,每个地区至少派遣一位专家,其中甲、乙两位专家需要派遣至同一地区,则不同的派遣方案种数有![]() 种;
种;
⑤已知双曲线![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 的直线交双曲线右支于
的直线交双曲线右支于![]() 两点,且
两点,且![]() ,若
,若![]() ,则双曲线的离心率为
,则双曲线的离心率为![]() .
.
其中正确的命题序号为_____.
参考答案:
【答案】②③⑤
【解析】
首先求出函数的定义域,求出函数的解析式,利用奇偶性的定义即可判断①;根据回归直线过样本中心点,代入即可判断②;利用正弦函数的性质,代入验证、整体代入即可判断③;利用分类计数原理以及组合数即可判断④;利用双曲线的定义以及离心率公式即可判断⑤.
①函数的定义域为![]() ,
,![]() ,既是奇函数又是偶函数,故错误;
,既是奇函数又是偶函数,故错误;
②根据回归直线方程恒过样本的中心点,将![]() 带入回归方程可得
带入回归方程可得![]() ,故正确;
,故正确;
③把![]() 代入函数
代入函数![]() ,函数值为
,函数值为![]() ,所以函数
,所以函数![]() 关于
关于![]() 对称,由
对称,由![]() ,可得函数
,可得函数![]() 的单调递增区间为
的单调递增区间为![]() ,所以函数
,所以函数![]() 在
在![]() 上是递增的.故正确;
上是递增的.故正确;
④根据题意,分![]() 种情况讨论,第一种:
种情况讨论,第一种:![]() 人分成
人分成![]() 的三组,
的三组,
仅甲乙![]() 人分到同一个地区,在
人分到同一个地区,在![]() 个地区中任选
个地区中任选![]() 个,安排甲乙,有
个,安排甲乙,有![]() 种情况,
种情况,
将剩下的![]() 人分成
人分成![]() 组,有
组,有![]() 种分组方法,将
种分组方法,将![]() 组全排列,安排到其他
组全排列,安排到其他![]() 个地区,
个地区,
有![]() 种情况,则此时有
种情况,则此时有![]() 种安排方法;
种安排方法;
第二种:![]() 人分成
人分成![]() 的三组,甲乙与其他三人中的
的三组,甲乙与其他三人中的![]() 人,一起安排到同一个区域,
人,一起安排到同一个区域,
在其他![]() 人中任选
人中任选![]() 人,与甲乙一起安排到一个地区,有
人,与甲乙一起安排到一个地区,有![]()
![]() 种情况,
种情况,
将剩下的![]() 人全排列,安排到其他
人全排列,安排到其他![]() 个地区,有
个地区,有![]() 种情况,
种情况,
则此时有![]() 种安排方法;则一共有
种安排方法;则一共有![]() 种安排方法.故错误.
种安排方法.故错误.
⑤设![]() 为双曲线右支上一点,由
为双曲线右支上一点,由![]() ,
,![]() ,
,

在直角三角形![]() 中,
中,![]() ,
,
由双曲线的定义可知:![]() ,
,
由![]() ,即有
,即有![]() ,
,
即为![]() ,
,
![]()
![]() ,解得
,解得![]() .
.
![]()
![]() ,
,
由勾股定理可得:![]() ,则
,则![]() .故正确.
.故正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】城南中学九年级共有12个班,每班48名学生,学校对该年级学生数学学科学业水平测试成绩进行了抽样分析,请按要求回答下列问题:
【收集数据】
(1)要从九年级学生中抽取一个48人的样本,你认为以下抽样方法中最合理的是
________.①随机抽取一个班级的48名学生;②在九年级学生中随机抽取48名女学生;
③在九年级12个班中每班各随机抽取4名学生.
【整理数据】
(2)将抽取的48名学生的成绩进行分组,绘制成绩频数分布表和成绩分布扇形统计图如下.
请根据图表中数据填空:
①表中m的值为________;
② B类部分的圆心角度数为________°;
③估计C、D类学生大约一共有_________名.

九年级学生数学成绩频数分布表
成绩(单位:分)
频数
频率
A类(80~100)
24

B类(60~79)
12
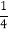
C类(40~59)
8
m
D类(0~39)
4
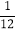
【分析数据】
(3)教育主管部们为了解学校学生成绩情况,将同层次的城南、城北两所中学的抽样数据进行对比分析,得到下表:
学校
平均数(分)
方差
A、B类的频率和
城南中学
71
358
0.75
城北中学
71
588
0.82
请你评价这两所学校学生数学学业水平测试的成绩,提出一个解释来支持你的观点.
-
科目: 来源: 题型:
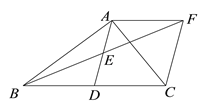
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,求证:四边形ADCF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】生活中处处有数学,下列原理运用错误的是
 .
.A.建筑工人砌墙时拉的参照线是运用“两点之间线段最短”的原理
B.修理损坏的椅子腿时斜钉的木条是运用“三角形稳定性”的原理
C.测量跳远的成绩是运用“垂线段最短”的原理
D.将车轮设计为圆形是运用了“圆的旋转对称性”原理
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校假期由校长带领该校“三好学生”去旅游,甲旅行社说“若校长买全票一张,则学生半价.”乙旅行社说“全部人六折优惠”若全票价是1200元,则:
(1)若学生人数是20人,甲、乙旅行社收费分别是多少?
(2)当学生人数的多少时,两家旅行社的收费一样?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为丰富学生课余生活,我校准备开设兴趣课堂.为了了解学生对绘画、书法、舞蹈、乐器这四个兴趣小组的喜爱情况,在全校进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息尚不完整),请根据图中提供的信息,解答下面的问题:

(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中乐器部分的圆心角的度数;
(3)如果我校共有1000名学生参加这4个课外兴趣小组,而每个教师最多只能辅导本组的25名学生,估计书法兴趣小组至少需要准备多少名教师?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在建筑物AB上,挂着35 m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A处,仰角为45°,看条幅底端E处,俯角为37°.求两建筑物间的距离BC.
(参考数据:sin37°≈0.6,cos37°≈0.8, tan37°≈0.75)

相关试题

