【题目】甲、乙两列火车分别从A,B两城同时相向匀速驶出,甲车开往终点B城,乙车开往终点A城,乙车比甲车早到达终点;如图,是两车相距的路程d(千米)与行驶时间t(小时)的函数关系图象. 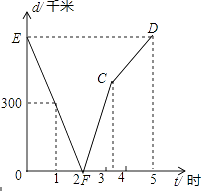
(1)A,B两城相距千米,经过小时两车相遇;
(2)分别求出甲、乙两车的速度;
(3)直接写出甲车距A城的路程S1、乙车距A城的路程S2与t的函数关系式;(不必写出t的范围)
(4)当两车相距100千米时,求t的值.
参考答案:
【答案】
(1)600;2
(2)解:甲车的速度为:600÷5=120(千米/时);
乙车的速度为:600÷2﹣120=180(千米/时).
答:甲车的速度为120千米/时,乙车的速度为180千米/时
(3)解:结合题意可知:s甲=120x,
s乙=600﹣180x
(4)解:两车第一次相距100千米的时间为:(600﹣100)÷(180+120)= ![]() (小时);
(小时);
两车第二次相距100千米的时间为:(600+100)÷(180+120)= ![]() (小时).
(小时).
∵180× ![]() =420(千米),420<600,
=420(千米),420<600,
∴第二次相距100千米时,乙车尚未到达终点,该时间符合题意.
答:当两车相距100千米路程时,t的值为 ![]() 小时或
小时或 ![]() 小时
小时
【解析】解:(1)观察函数图象可以发现: 当t=1时,d=300,而t=2时,d=0,
∴当t=0时,d=2×(300﹣0)=600.
∴A、B两地相距600千米.
当d=0时,t=2,
∴经过2小时两车相遇.
所以答案是:600,2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着几何部分的学习,小鹏对几何产生了浓厚的兴趣,他最喜欢利用手中的工具画图了
 如图,作一个
如图,作一个 ,以O为圆心任意长为半径画弧分别交OA,OB于点C和点D,将一副三角板如图所示摆放,两个直角三角板的直角顶点分别落在点C和点D,直角边中分别有一边与角的两边重合,另两条直角边相交于点P,连接
,以O为圆心任意长为半径画弧分别交OA,OB于点C和点D,将一副三角板如图所示摆放,两个直角三角板的直角顶点分别落在点C和点D,直角边中分别有一边与角的两边重合,另两条直角边相交于点P,连接 小鹏通过观察和推理,得出结论:OP平分
小鹏通过观察和推理,得出结论:OP平分 .
.你同意小鹏的观点吗?如果你同意小鹏的观点,试结合题意写出已知和求证,并证明.
已知:
 中,______
中,______ ______,______
______,______ ______,______
______,______ ______.
______.求证:OP平分
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,放在平面直角坐标系中的圆O的半径为3,现做如下实验:抛掷一枚均匀的正四面体骰子,它有四个顶点,各顶点数分别是1,2,3,4,每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的点数作为直角坐标系中点P的坐标(第一次的点数为横坐标,第二次的点数为纵坐标).
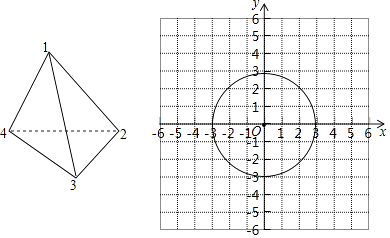
(1)若第一次骰子朝上的点数为1,第二次骰子朝上的点数为2,此时点P(填“是”或“否”)落在圆O内部;
(2)请你用树状图或列表的方法表示出P点坐标的所有可能结果;
(3)求点P落在圆O面上(含内部与边界)的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】边长为1的小正方形网格中,点A,B,C均落在格点上.
(1)猜想△ABC的形状 ,并证明;
(2)直接写出△ABC的面积= ;
(3)画出△ABC关于直线l的轴对称图形△A1B1C1.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数a,我们规定:用符号[
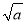 ]表示不大于
]表示不大于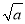 的最大整数,称[
的最大整数,称[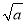 ]为a的根整数,例如:[
]为a的根整数,例如:[ ]=3,[
]=3,[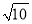 ]=3.
]=3.(1)仿照以上方法计算:[
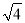 ] = ;[
] = ;[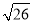 ] = .
] = .(2)若[
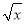 ]=1,写出满足题意的x的整数值 .
]=1,写出满足题意的x的整数值 .如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次 [
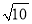 ]=3→[
]=3→[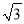 ]=1,这时候结果为1.
]=1,这时候结果为1.(3)对100连续求根整数, 次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,以BC为边作等边△BDC,连接AD.
(1)如图1,直接写出∠ADB的度数 ;
(2)如图2,作∠ABM=60°在BM上截取BE,使BE=BA,连接CE,判断CE与AD的数量关系,请补全图形,并加以证明;
(3)在(2)的条件下,连接DE,AE.若∠DEC=60°,DE=2,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】国家八纵八横高铁网络规划中“京昆通道”的重要组成部分──西成高铁于2017年12月6日开通运营,西安至成都列车运行时间由14小时缩短为3.5小时.张明和王强相约从成都坐高铁到西安旅游.如图,张明家(记作A)在成都东站(记作B)南偏西30°的方向且相距4000米,王强家(记作C)在成都东站南偏东60°的方向且相距3000米,则张明家与王强家的距离为( )
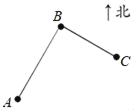
A. 6000米 B. 5000米 C. 4000米 D. 2000米
相关试题

