【题目】在△ABC中,AB=AC,以BC为边作等边△BDC,连接AD.
(1)如图1,直接写出∠ADB的度数 ;
(2)如图2,作∠ABM=60°在BM上截取BE,使BE=BA,连接CE,判断CE与AD的数量关系,请补全图形,并加以证明;
(3)在(2)的条件下,连接DE,AE.若∠DEC=60°,DE=2,求AE的长.

参考答案:
【答案】(1)150°;(2)CE=AD,证明详见解析;(3)AE=![]() .
.
【解析】
(1)只要根据已知条件易证△ADB≌△ADC,由全等三角形的性质可得∠ADB=∠ADC,根据周角的定义即可求得∠ADB的度数;(2)结论为CE=AD,证明△ABD≌△EBC,根据全等三角形的性质即可证得结论;(3)证明△BDE是直角三角形,△ABE是等边三角形即可解决问题;
解:(1)如图1中,

∵△BDC是等边三角形,
∴BD=DC,∠BDC=60°,
在△ADB和△ADC中,
 ,
,
∴△ADB≌△ADC,
∴∠ADB=∠ADC,
∵∠ADB+∠ADC=360°﹣60°,
∴∠ADB=150°,
故答案为150°.
(2)结论:CE=AD.

理由:∵∠ABE=∠DBC=60°
∴∠ABE﹣∠DBM=∠DBC﹣∠DBM
∴∠1=∠2,
∵AB=BE,BD=DC
∴△ABD≌△EBC
∴CE=AD.
(3)解:

∵△ABD≌△EBC
∴∠BCE=∠BDA=150°
∵∠DCE=90°,∠DEC=60°
∴∠CDE=30°
∵DE=2
∴CE=1,DC=BC=![]() ,
,
∵∠BDE=60°+30°=90°
DE=2,BD=![]()
由勾股BE=![]() ,
,
∵∠ABE=60°AB=BE
∴△ABE是等边三角形
∴AE=BE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】边长为1的小正方形网格中,点A,B,C均落在格点上.
(1)猜想△ABC的形状 ,并证明;
(2)直接写出△ABC的面积= ;
(3)画出△ABC关于直线l的轴对称图形△A1B1C1.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两列火车分别从A,B两城同时相向匀速驶出,甲车开往终点B城,乙车开往终点A城,乙车比甲车早到达终点;如图,是两车相距的路程d(千米)与行驶时间t(小时)的函数关系图象.
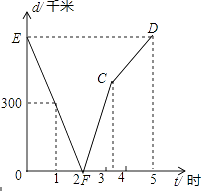
(1)A,B两城相距千米,经过小时两车相遇;
(2)分别求出甲、乙两车的速度;
(3)直接写出甲车距A城的路程S1、乙车距A城的路程S2与t的函数关系式;(不必写出t的范围)
(4)当两车相距100千米时,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数a,我们规定:用符号[
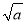 ]表示不大于
]表示不大于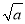 的最大整数,称[
的最大整数,称[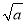 ]为a的根整数,例如:[
]为a的根整数,例如:[ ]=3,[
]=3,[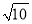 ]=3.
]=3.(1)仿照以上方法计算:[
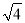 ] = ;[
] = ;[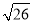 ] = .
] = .(2)若[
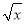 ]=1,写出满足题意的x的整数值 .
]=1,写出满足题意的x的整数值 .如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次 [
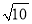 ]=3→[
]=3→[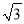 ]=1,这时候结果为1.
]=1,这时候结果为1.(3)对100连续求根整数, 次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家八纵八横高铁网络规划中“京昆通道”的重要组成部分──西成高铁于2017年12月6日开通运营,西安至成都列车运行时间由14小时缩短为3.5小时.张明和王强相约从成都坐高铁到西安旅游.如图,张明家(记作A)在成都东站(记作B)南偏西30°的方向且相距4000米,王强家(记作C)在成都东站南偏东60°的方向且相距3000米,则张明家与王强家的距离为( )
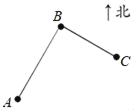
A. 6000米 B. 5000米 C. 4000米 D. 2000米
-
科目: 来源: 题型:
查看答案和解析>>【题目】现在,苏宁商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果商场还能盈利25%,这台冰箱的进价是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )

A. 1组 B. 2组 C. 3组 D. 4组
相关试题

