【题目】对于实数a,我们规定:用符号[![]() ]表示不大于
]表示不大于![]() 的最大整数,称[
的最大整数,称[![]() ]为a的根整数,例如:[
]为a的根整数,例如:[![]() ]=3,[
]=3,[![]() ]=3.
]=3.
(1)仿照以上方法计算:[![]() ] = ;[
] = ;[![]() ] = .
] = .
(2)若[![]() ]=1,写出满足题意的x的整数值 .
]=1,写出满足题意的x的整数值 .
如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次 [![]() ]=3→[
]=3→[![]() ]=1,这时候结果为1.
]=1,这时候结果为1.
(3)对100连续求根整数, 次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是 .
参考答案:
【答案】(1)2,5;(2)1,2,3;(3)3;(4)最大的正整数是255,理由见解析
【解析】试题分析:(1)阅读上面的文件,仿照例子写出答案;
(2)根据题意,平方的数值范围,结合例子写出范围内的单即可;
(3)根据题意一次求出100的求根结果;
(4)由题意直接判断连续求根,确定最大数值即可.
试题解析:(1)∵22=4,52=25,62=36,
∴5<![]() <6,
<6,
∴![]() =[2]=2,[
=[2]=2,[![]() ]=5,
]=5,
故答案为:2,5;
(2)∵12=1,22=4,且![]() =1,
=1,
∴x=1,2,3,
故答案为:1,2,3;
(3)第一次:[![]() ]=10,
]=10,
第二次:[![]() ]=3,
]=3,
第三次:[![]() ]=1,
]=1,
故答案为:3;
(4)最大的正整数是255,
理由是:∵[![]() ]=15,[
]=15,[![]() ]=3,[
]=3,[![]() ]=1,
]=1,
∴对255只需进行3次操作后变为1,
∵[![]() ]=16,[
]=16,[![]() ]=4,[
]=4,[![]() ]=2,[
]=2,[![]() ]=1,
]=1,
∴对256只需进行4次操作后变为1,
∴只需进行3次操作后变为1的所有正整数中,最大的是255,
故答案为:255.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)
解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= ( )
∴ ∥ ,( )
∴∠AGD+ =180°,(两直线平行,同旁内角互补)
∵ ,(已知)
∴∠AGD= (等式性质)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线L;y=ax2+bx+c(其中a、b、c都不等于0), 它的顶点P的坐标是
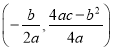 ,与y轴的交点是M(0,c)我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.
,与y轴的交点是M(0,c)我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.(1)请直接写出抛物线y=2x2-4x+1的伴随抛物线和伴随直线的关系式:
伴随抛物线的关系式_________________
伴随直线的关系式___________________
(2)若一条抛物线的伴随抛物线和伴随直线分别是y=-x2-3和y=-x-3, 则这条抛物线的关系是___________:
(3)求抛物线L:y=ax2+bx+c(其中a、b、c都不等于0) 的伴随抛物线和伴随直线的关系式;
(4)若抛物线L与x轴交于A(x1,0),B(x2,0)两点x2>x1>0,它的伴随抛物线与x 轴交于C,D两点,且AB=CD,请求出a、b、c应满足的条件.
-
科目: 来源: 题型:
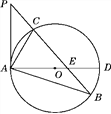
查看答案和解析>>【题目】如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长;(3)在满足(2)的条件下,若AF∶FD=1∶2,GF=1,求⊙O的半径及sin∠ACE的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,美丽的弦图,蕴含着四个全等的直角三角形.
(1)弦图中包含了一大,一小两个正方形,已知每个直角三角形较长的直角边为
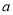 ,较短的直角边为
,较短的直角边为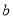 ,斜边长为
,斜边长为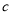 ,试利用图①验证勾股定理;
,试利用图①验证勾股定理;(2)如图②,将这四个全等的直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(实线)的周长为
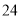 ,
, 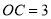 ,求该飞镖状图案的面积;
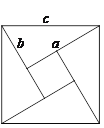
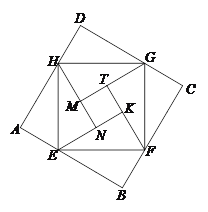
,求该飞镖状图案的面积;(3)如图③,将八个全等的直角三角形紧密地拼接,记图中正方形
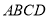 ,正方形
,正方形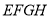 ,正方形
,正方形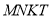 的面积分别为
的面积分别为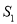 ,
, 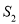 ,
, 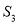 ,若
,若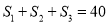 ,则
,则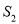 =________.
=________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】利用我们学过的知识,可以导出下面这个形式优美的等式:
a2+b2+c2-ab-bc-ac=
 [(a-b)2+(b-c)2+(c-a)2],
[(a-b)2+(b-c)2+(c-a)2],该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.
(1)请你检验这个等式的正确性;
(2)若a=2 016,b=2 017,c=2 018,你能很快求出a2+b2+c2-ab-bc-ac的值吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索:
(x-1)(x+1)=x2-1, (x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1, (x-1)(x4+x3+x2+x+1)=x5-1,
……
(1)试写出第五个等式;
(2)试求26+25+24+23+22+2+1的值;
(3)判断22 017+22 016+22 015+…+22+2+1的值的个位数字是几.
相关试题

