【题目】(本题满分12分)如图,Rt△![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为斜边
为斜边![]() 的中点,点
的中点,点![]() 为边
为边![]() 上的一个动点.连结
上的一个动点.连结![]() ,过点
,过点![]() 作
作![]() 的垂线与边
的垂线与边![]() 交于点
交于点![]() ,以
,以![]() 为邻边作矩形
为邻边作矩形![]() .
.
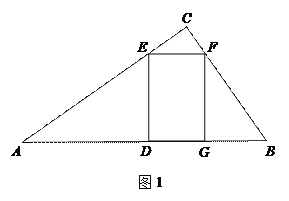
(1)如图1,当![]() ,点
,点![]() 在边
在边![]() 上时,求DE和EF的长;
上时,求DE和EF的长;
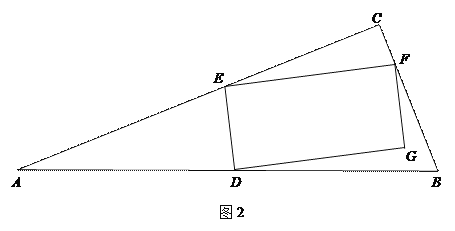
(2)如图2,若![]() ,设
,设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() ,求y关于
,求y关于![]() 的函数表达式;
的函数表达式;
(3)若![]() ,且点
,且点![]() 恰好落在Rt△
恰好落在Rt△![]() 的边上,求
的边上,求![]() 的长.
的长.
参考答案:
【答案】(1)![]() ;
; ![]() ;(2)
;(2)![]() ;(3)9或12.
;(3)9或12.
【解析】试题分析:(1)根据勾股定理求出AB,根据相似三角形的判定定理得到△ADE∽△ACB,根据相似三角形的性质求出DE和BG,求出EF;
(2)作DH⊥AC于H,根据相似三角形的性质得到y关于x的函数解析式;
(3)根据点G在边BC上和点G在边AB上两种情况,根据相似三角形的性质解答.
解:(1)∵∠ACB=90°,BC=6,AC=8,
∴AB= =10,
∵D为斜边AB的中点,
∴AD=BD=5,
∵DEFG为矩形,
∴∠ADE=90°,
∴∠ADE=∠C,又∠A=∠A,
∴△ADE∽△ACB,
∴AD:AC=DE:BC,即5:8=DE:6,
解得,DE=![]() ,
,
∵△ADE∽△FGB,
∴AD:GF=DE:BG,
则BG=![]() ,
,
∴EF=DG=AB-AD-BG=![]() ;
;
(2)过点![]() 作
作![]() 于点
于点![]() , 从而
, 从而![]() .
.
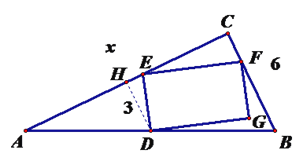
易得△![]() ∽△
∽△![]() ,
,
由![]() , 可得
, 可得![]() ,
, ![]() .
.
所以![]() .
.
∴![]() .
.
(3)由题意,点![]() 可以在边
可以在边![]() 或者
或者![]() 上.
上.
①若点![]() 在边
在边![]() 上,
上,
由![]() ,可知
,可知![]() ,于是
,于是![]() ;
;
②若点![]() 在边
在边![]() 上.
上.
记![]() ,矩形边长
,矩形边长![]() ,
,
由△![]() ∽△
∽△![]() , 可得
, 可得![]() , 即
, 即![]() ,
,
化简可得![]() , 因式分解后有:
, 因式分解后有: ![]() , 即
, 即![]() .
.
而由△![]() ∽△
∽△![]() , 所以
, 所以![]() , 从而
, 从而![]() .
.
综上知,AC的值为9或12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.
(1)求证:AC是⊙O的切线;
(2)若sinC=
 ,AC=6,求⊙O的直径.
,AC=6,求⊙O的直径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出
某商店经销《超能陆战队》超萌“小白”(图1)玩具,“小白”玩具每个进价60元.为进行促销,商店制定如下“优惠”方案:如果一次销售数量不超过10个,则销售单价为100元/个;如果一次销售数量超过10个,每增加一个,所有“小白”玩具销售单价降低1元/个,但单价不得低于80元/个.一次销售“小白”玩具的单价y(元/个)与销售数量x(个)之间的函数关系如图2所示.

(1)求m的值并解释射线BC所表示的实际意义;
(2)写出该店当一次销售x个时,所获利润w(元)与x(个)之间的函数关系式;
(3)店长经过一段时间的销售发现:即并不是销量越大利润越大(比如,卖25个赚的钱反而比卖30个赚的钱多).为了不出现这种现象,在其他条件不变的情况下,店长应把原来的最低单价80(元/个)至少提高到多少元/个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三位数,个位、十位上的数的和比百位上的数小 2,十位上的数的 3 倍比百位、个位上的数的和大 4,且个位、十位、百位上的数的和是 8,则这个三位数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空,如图,已知∠A=∠F,∠C=∠D,试说明 BD∥CE.

解:∵∠A=∠F(已知),
∴ ∥ ( ),
∴∠D+∠DBC=180°( ),
又∵∠C=∠D(已知),
∴∠C+∠DBC=180°(等量代换),
∴BD∥CE( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)一种商品有大小两种包装,4 大盒、3 小盒共装 116 瓶;3 大盒、2 小盒共装 84 瓶,求大盒与小盒每盒各装多少瓶?
(2)一种商品有大中小三种包装,4 大盒、2 中盒、3 小盒共装 137 瓶;3 大盒、5 中盒、4 小盒共装171 瓶,一个顾客买了这种商品大中小各两盒,请问这个顾客买了这种商品多少瓶?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三名射箭运动员在某次测试中各射箭8次,三人的测试成绩如下表:
s2甲、s 2乙、s 2丙分别表示三名运动员这次测试成绩的方差,下面各式中正确的是( )

A. s 2甲>s 2乙>s 2丙 B. s 2丙>s 2乙>s 2甲
C. s 2丙>s 2甲>s 2乙 D. s 2乙>s 2甲>s 2丙
相关试题

