【题目】如图,抛物线y=ax2﹣2x+c(a≠0)与x轴、y轴分别交于点A,B,C三点,已知点A(﹣2,0),点C(0,﹣8),点D是抛物线的顶点.
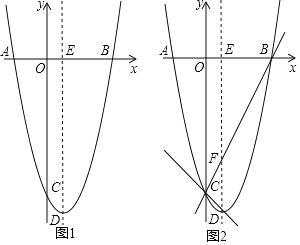
(1)求抛物线的解析式及顶点D的坐标;
(2)如图1,抛物线的对称轴与x轴交于点E,第四象限的抛物线上有一点P,将△EBP沿直线EP折叠,使点B的对应点B'落在抛物线的对称轴上,求点P的坐标;
(3)如图2,设BC交抛物线的对称轴于点F,作直线CD,点M是直线CD上的动点,点N是平面内一点,当以点B,F,M,N为顶点的四边形是菱形时,请直接写出点M的坐标.
参考答案:
【答案】(1)y=x2﹣2x﹣8,D(1,﹣9);(2)P(![]() ,
, ![]() );(3)点M的坐标为(﹣
);(3)点M的坐标为(﹣![]() ,
, ![]() )或(4,﹣12)或(﹣5,﹣3).
)或(4,﹣12)或(﹣5,﹣3).
【解析】试题分析:(1)将点A、点C的坐标代入抛物线的解析式可求得a、c的值,从而得到抛物线的解析式,最后利用配方法可求得点D的坐标;
(2)将y=0代入抛物线的解析式求得点B的坐标,然后由抛物线的对称轴方程可求得点E的坐标,由折叠的性质可求得∠BEP=45°,设直线EP的解析式为y=﹣x+b,将点E的坐标代入可求得b的值,从而可求得直线EP的解析式,最后将直线EP的解析式和抛物线的解析式联立组成方程组求解即可;
(3)先求得直线CD的解析式,然后再求得直线CB的解析式为y=k2x﹣8,从而可求得点F的坐标,设点M的坐标为(a,﹣a﹣8),然后分为MF=MB、FM=FB两种情况列方程求解即可.
试题解析:(1)将点A、点C的坐标代入抛物线的解析式得: ![]() ,解得:a=1,c=﹣8,∴抛物线的解析式为
,解得:a=1,c=﹣8,∴抛物线的解析式为![]() .∵y=(x﹣1)2﹣9,∴D(1,﹣9);
.∵y=(x﹣1)2﹣9,∴D(1,﹣9);
(2)将y=0代入抛物线的解析式得:x2﹣2x﹣8=0,解得x=4或x=﹣2,∴B(4,0),
∵y=(x﹣1)2﹣9,∴抛物线的对称轴为x=1,∴E(1,0),
∵将△EBP沿直线EP折叠,使点B的对应点B'落在抛物线的对称轴上,∴EP为∠BEF的角平分线,∴∠BEP=45°,
设直线EP的解析式为y=﹣x+b,将点E的坐标代入得:﹣1+b=0,解得b=1,
∴直线EP的解析式为y=﹣x+1.将y=﹣x+1代入抛物线的解析式得: ![]() ,解得:x=
,解得:x=![]() 或x=
或x=![]() ,
,
点P在第四象限,∴x=![]() ,∴y=
,∴y=![]() ,∴P(
,∴P(![]() ,
, ![]() );
);
(3)设CD的解析式为y=kx﹣8,将点D的坐标代入得:k﹣8=﹣9,解得k=﹣1,
∴直线CD的解析式为y=﹣x﹣8,
设直线CB的解析式为y=k2x﹣8,将点B的坐标代入得:4k2﹣8=0,解得:k2=2,
∴直线BC的解析式为y=2x﹣8,
将x=1代入直线BC的解析式得:y=﹣6,∴F(1,﹣6),
设点M的坐标为(a,﹣a﹣8),
当MF=MB时,(a﹣4)2+(a+8)2=(a﹣1)2+(a+2)2,整理得:6a=﹣75,解得:a=﹣![]() ,∴点M的坐标为(﹣
,∴点M的坐标为(﹣![]() ,
, ![]() );
);
当FM=FB时,(a﹣1)2+(a+2)2=(4﹣1)2+(﹣6﹣0)2,整理得:a2+a﹣20=0,解得:a=4或a=﹣5,
∴点M的坐标为(4,﹣12)或(﹣5,﹣3);
综上所述,点M的坐标为(﹣![]() ,
, ![]() )或(4,﹣12)或(﹣5,﹣3).
)或(4,﹣12)或(﹣5,﹣3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品A的零售价为每件900元,为了适应市场竞争,商店按零售价的九折优惠后,再让利40元销售,仍可获利10%.
(1)这种商品A的进价为多少元?
(2)现有另一种商品B进价为600元,每件商品B也可获利10%.对商品A和B共进货100件,要使这100件商品共获纯利6670元,则需对商品A、B分别进货多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分)
中位数(分)
众数(分)
方差(
 )
)初中部
a
85
b

高中部
85
c
100
160
(1)根据图示计算出a、b、c的值;
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算初中代表队决赛成绩的方差
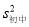 ,并判断哪一个代表队选手成绩较为稳定.
,并判断哪一个代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式1+2xy﹣3xy2的次数及项数分别是( )
A.5,3B.2,3C.5,2D.3,3
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国最长的河流长江全长约6300千米,6300千米用科学记数法表示为( )
A.6.3×102千米B.6.3×103千米
C.0.63×104千米D.630×10千米
-
科目: 来源: 题型:
查看答案和解析>>【题目】在7x2﹣4x+1﹣x2﹣2+6x中,7x2与_____是同类项,6x与_____是同类项,﹣2与____是同类项.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍.
(1)求降价后每枝玫瑰的售价是多少元?
(2)根据销售情况,店主用不多于900元的资金再次购进两种鲜花共500枝,康乃馨进价为2元/枝,玫瑰进价为1.5元/枝,问至少购进玫瑰多少枝?
相关试题

