【题目】图a是一个长为2 m、宽为2 n的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图b的形状拼成一个正方形。
(1)你认为图b中的阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图中阴影部分的面积。


方法1:
方法2:
(3)观察图b你能写出下列三个代数式之间的等量关系吗?
代数式: ![]()
(4)根据(3)题中的等量关系,解决如下问题:
若![]() ,则
,则![]() = 。
= 。
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() =
= ![]() ;(4)29
;(4)29
【解析】分析:
(1)由题中的已知数量结合图形即可得到图b中阴影部分正方形的边长;
(2)①由(1)中所得阴影部分正方形的边长可表达出其面积;②由已知条件结合图形可得图b中大正方形的边长为(m+n),由大正方形的面积减去4个小矩形的面积可得阴影部分的面积;
(3)由(2)中阴影部分小正方形面积的两种不同表示方法即可得到![]() 三个式子间的数量关系;
三个式子间的数量关系;
(4)应用(3)中所得数量关系进行解答即可.
详解:
(1)由题意可得图b中阴影部分的小正方形的边长为: ![]() ;
;
(2)方法1:由(1)可知阴影部分的小正方形的边长为![]() ,
,
∴阴影部分小正方形的面积为: ![]() ;
;
方法2:由题意可得图b中大正方形的边长为: ![]() ,
,
∴阴影部分小正方形的面积为: ![]() ;
;
(3)由(2)可得:小正方形的面积=![]() =
=![]() ,
,
∴![]() 三个式子间的数量关系为:
三个式子间的数量关系为: ![]() =
=![]() ;
;
(4)∵![]() ,
,
∴由(3)中所得数量关系可得: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,纸片□ABCD中,AD=5,S□ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为( )
A.平行四边形 B.菱形 C.矩形 D.正方形
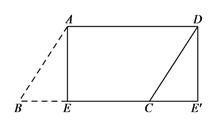
(2)如图,在(1)中的四边形纸片AEE'D中,在EE'上取一点F,使EF=4,剪下△AEF,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形AFF'D.
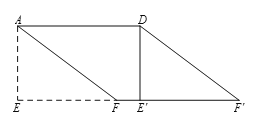
①求证:四边形AFF'D是菱形;
②求四边形AFF'D的两条对角线的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C,D在⊙O上,点O在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
 的图像如图所示,点A0位于坐标原点,点A1 , A2 , A3 , …,A2008在y轴的正半轴上,点B1 , B2 , B3 , …,B2008在二次函数
的图像如图所示,点A0位于坐标原点,点A1 , A2 , A3 , …,A2008在y轴的正半轴上,点B1 , B2 , B3 , …,B2008在二次函数  位于第一象限的图像上,若△A0B1A1 , △A1B2A2 , △A2B3A3 , …,△A2007B2008A2008都为等边三角形,则△A2007B2008A2008的边长=
位于第一象限的图像上,若△A0B1A1 , △A1B2A2 , △A2B3A3 , …,△A2007B2008A2008都为等边三角形,则△A2007B2008A2008的边长=
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按HUI图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2018个点的坐标为___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:

对这两名运动员的成绩进行比较,下列四个结论中,不正确的是( )
A. 甲运动员得分的极差大于乙运动员得分的极差
B. 甲运动员得分的中位数大于乙运动员得分的中位数
C. 甲运动员得分的平均数大于乙运动员得分的平均数
D. 甲运动员的成绩比乙运动员的成绩稳定
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知小敏家距学校5km,小飞家距小敏家3km.若小飞家距学校距离为xkm,则x满足( )
A.x=2B.2≤x≤8C.2≤x≤5D.2<x<8
相关试题

