【题目】![]() 如图
如图![]() ,在
,在![]() 中,
中,![]() ,若
,若![]() 是
是![]() 和
和![]() 的平分线交点,求
的平分线交点,求![]() 的度数。
的度数。

![]() 若是内任意一点,试探究
若是内任意一点,试探究![]() 与
与![]() 之间的关系,并说明理由
之间的关系,并说明理由

![]() 请你直接利用以上结论,解决以下问题:
请你直接利用以上结论,解决以下问题:
①图![]() 中点
中点![]() 为
为![]() 内任意一点,若
内任意一点,若![]() 则
则![]()
![]()

②如图![]() 平分
平分![]() 平分
平分![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.

参考答案:
【答案】(1)∠BDC=125°;(2)∠BDC=∠BAC+∠ABD+∠ACD,理由见解析;(3)①60;②∠DCE=90°.
【解析】
(1)根据三角形的内角和与DB平分∠ABC,DC平分∠ACB可求得∠DBC+∠DCB的度数,再在△DBC中应用三角形内角和定理即可求出结果;
(2)作射线AD,再运用三角形的外角性质即可得出结论;
(3)①直接应用(2)的结论计算即可;
②先由(2)的结论求出∠ADB+∠AEB的度数,再由CD平分∠ADB,CE平分∠ACB可求出∠ADC+∠AEC的度数,然后再运用(2)的结论即可求出结果.
解:(1)∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=180°-70°=110°,
∵DB平分∠ABC,DC平分∠ACB,
∴∠DBC=![]() ∠ABC,∠DCB=
∠ABC,∠DCB=![]() ∠ACB,
∠ACB,
∴∠DBC+∠DCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×110°=55°,
×110°=55°,
∴∠BDC=180°-55°=125°;
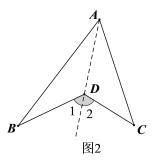
(2)∠BDC=∠BAC+∠ABD+∠ACD,理由如下:
如图2,作射线AD,∵∠1、∠2分别是△ABD和△ACD的外角,
∴∠1=∠BAD+∠ABD,∠2=∠CAD+∠ACD,
∴∠BDC=∠1+∠2=∠BAD+∠ABD+∠CAD+∠ACD=∠BAC+∠ABD+∠ACD.
(3)①由(2)的结论可得:∠ABD+∠ACD=∠BDC―∠A=110°-50°=60°;故答案为60;
②由(2)的结论可得:∠ADB+∠AEB=∠DBE―∠A=130°-50°=80°;
∵CD平分∠ADB,CE平分∠ACB,
∴∠ADC=![]() ∠ADB,∠AEC=
∠ADB,∠AEC=![]() ∠AEB,
∠AEB,
∴∠ADC+∠AEC=![]() (∠ADB+∠AEB)=
(∠ADB+∠AEB)=![]() ×80°=40°,
×80°=40°,
又∵∠DCE=∠ADC+∠A+∠AEC,
∴∠DCE=50°+40°=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是48cm,求:
(1)两条对角线的长度;
(2)菱形的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项,现随机抽查了m名学生,并将其结果绘制成如下不完整的条形图和扇形图.

请结合以上信息解答下列问题:
(1)m= ;
(2)请补全上面的条形统计图;
(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为 ;
(4)已知该校共有1200名学生,请你估计该校约有 名学生最喜爱足球活动.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(1)﹣28﹣(﹣19)+(﹣24)
(2)(﹣12)﹣(+8)﹣(+10)﹣(﹣8)
(3)2
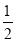 +(﹣
+(﹣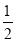 )﹣(﹣
)﹣(﹣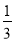 )+2
)+2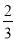
(4)
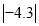 ﹣
﹣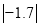 ﹣6.3.
﹣6.3. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架梯子AB长13米,斜靠在一面墙上,梯子底端离墙5米.(1)这个梯子的顶端距地面有多高?(2)如果梯子的顶端下滑了5米,那么梯子的底端在水平方向滑动了多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在纸面上有一数轴(如图),折叠纸面.
(1)若 1 表示的点与﹣1 表示的点重合,则﹣2 表示的点与数______表示的点重合;
(2)若﹣1 表示的点与 3 表示的点重合,
①那么 7 表示的点与数_______表示的点重合;
②若数轴上 A、B 两点之间的距离为 11(点 A 在点 B 的左侧),且 A、B 两点经折叠之后 重合,求 A、B 两点表示的数是多少.
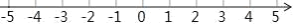
相关试题

