【题目】如图,Rt△ACB中,∠C=90°,AC=5cm,BC=2cm,点P从B点出发以1cm/s的速度沿CB延长线运动,运动时间为t秒.以AP为斜边在其上方构造等腰直角△APD.当t=1秒时,则CD=_____cm,当D运动的路程为4![]() cm时,则P运动时间t=_____秒.
cm时,则P运动时间t=_____秒.

参考答案:
【答案】4![]() 8
8
【解析】
连接CD,作DF⊥CB于F,DE⊥CA于E.首先证明AC+CB=![]() CD,延长即可解决问题;
CD,延长即可解决问题;
解:连接CD,作DF⊥CB于F,DE⊥CA于E.
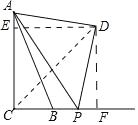
∵DA=DP,∠ADP=90°,
∴∠DAP=∠DPA=45°,
∵∠ACP+∠ADP=180°,
∴A,C,P,D四点共圆,
∴∠ACD=∠APD=45°,
∴∠ACD=∠DCF,
∵DE⊥CA,DF⊥CF,
∴DE=DF,
∵∠EDF=∠ADP=90°,
∴∠ADE=∠PDF,
∵∠DEA=∠DFP=90°,
∴△DEA≌△DFP(ASA),
∴AE=DF,
∵CD=CD,DE=DF,
∴Rt△CDE≌Rt△CDF(HL),
∴CE=DF,
∴四边形ECFD是正方形,
∴AC+CP=EC+AE+CF﹣PF=2EC=![]() CD,
CD,
∵t=1s时,AC=5cm,CP=3cm,
∴CD=![]() =4
=4![]() (cm),
(cm),
当t=0时,CD=![]() =
=![]() ,
,
当D运动的路程为4![]() cm时,CD=4
cm时,CD=4![]() +
+![]() =
=![]() ,
,
∵AC+CP=![]() CD,
CD,
∴5+CP=15,
∴CP=10,
∴PB=8,t=8.
故答案为:4![]() ;8.
;8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为( )

A.5
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示把多块大小不同的30°直角三角板,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与x轴重合且点A的坐标为(2,0),∠ABO=30°;第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交x轴于点B1;第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交y轴于点B2;第四块三角板斜边B2B3与第三块三角板的斜边B1B2垂直且交x轴于点B3;…按此规律继续下去,则点B2018的坐标为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上点
 在原点的左边,到原点的距离为4,点
在原点的左边,到原点的距离为4,点 在原点右边,从点
在原点右边,从点 走到点
走到点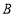 ,要经过16个单位长度.
,要经过16个单位长度.(1)写出
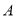 、
、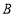 两点所对应的数;
两点所对应的数;(2)若点
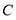 也是数轴上的点,点
也是数轴上的点,点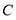 到点
到点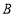 的距离是点
的距离是点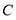 到原点距离的3倍,求
到原点距离的3倍,求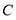 对应的数;
对应的数;(3)已知点
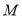 从点
从点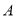 开始向右出发,速度每秒1个单位长度,同时
开始向右出发,速度每秒1个单位长度,同时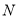 从
从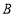 点开始向右出发,速度每秒2个单位长度,设线段
点开始向右出发,速度每秒2个单位长度,设线段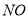 的中点为
的中点为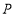 ,线段
,线段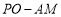 的值是否会发生变化?若会,请说明理由,若不会,请求出求其值.
的值是否会发生变化?若会,请说明理由,若不会,请求出求其值. -
科目: 来源: 题型:
查看答案和解析>>【题目】图1是由一副三角板拼成的图案,其中
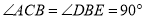 ,
,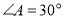 ,
,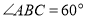 ,
,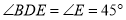 .
.(1)求图1中
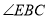 的度数;
的度数;(2)若将图1中的三角板
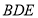 不动,将另一三角板
不动,将另一三角板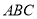 绕点
绕点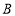 顺时针或逆时针旋转
顺时针或逆时针旋转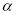 度(
度(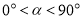 ).当
).当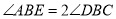 时,求
时,求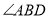 的度数(图2,图3,图4仅供参考).
的度数(图2,图3,图4仅供参考).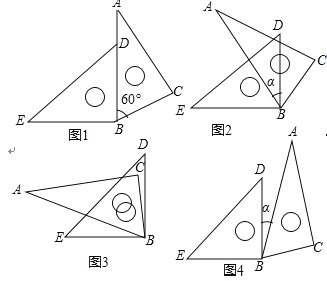
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为点G,连接CG,下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值
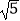 ﹣1.其中正确的说法有( )个.
﹣1.其中正确的说法有( )个.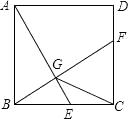
A.4
B.3
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为 .

相关试题

