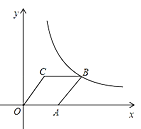
【题目】如图,菱形OABC的顶点C的坐标为(6,8).顶点A在x轴的正半轴上,反比例函数![]() 的图象经过顶B点.
的图象经过顶B点.
(1)求点A和B的坐标;
(2)求k值及直线AB对应的函数解析式.
参考答案:
【答案】(1)A(10,0),B(16,8);(2)k=128,![]() .
.
【解析】
(1)过C点作CD⊥x轴,垂足为D,从而得到OD=6,CD=8,再根据勾股定理求得OC=10,则有OC=BC=OA=10,即可写出点A和点B的坐标;
(2)将点B坐标代入反比例函数![]() 即可求得k的值;设直线AB的解析式为y=ax+b,将A、B两点坐标代入得到关于a、b的二元一次方程组,解方程组即可得到直线AB的解析式;
即可求得k的值;设直线AB的解析式为y=ax+b,将A、B两点坐标代入得到关于a、b的二元一次方程组,解方程组即可得到直线AB的解析式;
解:(1)过C点作CD⊥x轴,垂足为D,
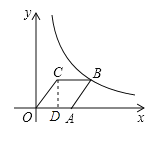
∵点C的坐标为(6,8),
∴OD=6,CD=8
∴OC=![]() =10
=10
∴OC=BC=OA=10,
∴点B(16,8),A(10,0);
(2)∵反比例函数![]() 的图象经过顶点B,
的图象经过顶点B,
∴8=![]() ,
,
∴k=128;
设直线AB的解析式为y=ax+b,
∵直线AB经过了点A(10,0)和点B(16,8),
∴![]() ,
,
∴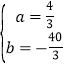 ,
,
∴直线AB解析式![]() .
.
-
科目: 来源: 题型:
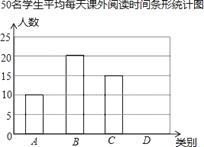
查看答案和解析>>【题目】某校为了了解学生课外阅读情况,随机抽查了50名学生,统计他们平均每天课外阅读时间(t小时).根据t的长短分为A,B,C,D四类,下面是根据所抽查的人数绘制的两幅不完整的统计图表.请根据图中提供的信息,解答下面的问题:
(1)求表格中的a的值,并在图中补全条形统计图;
(2)该校现有1300名学生,请你估计该校共有多少名学生课外阅读时间不少于1小时?50名学生平均每天课外阅读时间统计表
类别
时间t(小时)
人数
A
t<0.5
10
B
0.5≤t<1
20
C
1≤t<1.5
15
D
t≥1.5
a
-
科目: 来源: 题型:
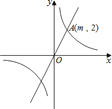
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,正比例函数y=kx的图象与反比例函数
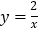 的图象有一个交点A(m,2).
的图象有一个交点A(m,2).(1)求m的值及正比例函数y=kx的解析式;
(2)试判断点B(2,3)是否在正比例函数图象上,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在两建筑物之间有一根高15米的旗杆,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°.若旗杆底点G为BC的中点,则矮建筑物的高CD为( )
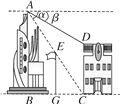
A. 20米 B. 10
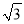 米 C. 15
米 C. 15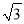 米 D. 5
米 D. 5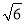 米
米 -
科目: 来源: 题型:
查看答案和解析>>【题目】观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游,不同租赁公司的租车费用(单位:元)与时间(单位:
 )之间的关系如图所示.
)之间的关系如图所示.
根据以上信息,解答下列问题:
(1)设租车时间为
 时,租用甲公司的车所需费用为
时,租用甲公司的车所需费用为 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 元,分别求出
元,分别求出 ,
, 关于
关于 的函数解析式;
的函数解析式;(2)请你帮助小明计算并选择哪个出游方案合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,点A、B分别在函数y1=
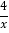 (x>0)与y2=
(x>0)与y2=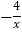 (x<0)的图象上,A、B的横坐标分别为a、b.
(x<0)的图象上,A、B的横坐标分别为a、b.(1)若AB∥x轴,求△OAB的面积;
(2)若△OAB是以AB为底边的等腰三角形,且a+b
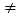 0,求ab的值;
0,求ab的值;(3)作边长为3的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,对大于或等于4的任意实数a,CD边与函数y1=
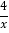 (x>0)的图象都有交点,请说明理由.
(x>0)的图象都有交点,请说明理由.
相关试题

