【题目】为了创建国家卫生城市,需要购买甲、乙两种类型的分类垃圾桶替换原来的垃圾桶,![]() ,
,![]() ,
,![]() 三个小区所购买的数量和总价如表所示.
三个小区所购买的数量和总价如表所示.
甲型垃圾桶数量(套) | 乙型垃圾桶数量(套) | 总价(元) | |
|
|
|
|
|
|
|
|
|
|
|
|
(1)问甲型垃圾桶、乙型垃圾桶的单价分别是每套多少元?
(2)求![]() ,
,![]() 的值.
的值.
参考答案:
【答案】(1)![]() ,(2)
,(2)![]() 或
或![]() .
.
【解析】
(1)设甲型垃圾桶的单价是x元/套,乙型垃圾桶的单价是y元/套.根据图表中的甲型、乙型垃圾桶的数量和它们的总价列出方程组并解答.
(2)根据图表中的数据列出关于a、b的二元一次方程,结合a、b的取值范围来求它们的值即可.
解:(1)设甲型垃圾桶的单价是x元/套,乙型垃圾桶的单价是y元/套.
依题意得:![]() ,
,
解得![]() .
.
答:甲型垃圾桶的单价是140元/套,乙型垃圾桶的单价是240元/套.
(2)由题意得:140a+240b=2580,
整理,得 7a+12b=129,
因为a、b都是正整数,
所以![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形 ABCD为⊙O的内接四边四边形,已知∠BOD=100°,则∠BCD 的度数为( )

A.50°
B.80°
C.100°
D.130° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x、y的方程组
 ,给出下列结论:
,给出下列结论:①
 是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;
是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④x,y的都为自然数的解有4对.
其中正确的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点 A 、B分别在反比例函数
 的图象上,且OA ⊥OB ,则
的图象上,且OA ⊥OB ,则  的值为( )
的值为( )
A.
B.2
C.
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax
 +bx+c经过点(-1,0),对称轴l如图所示.则下列结论:①
+bx+c经过点(-1,0),对称轴l如图所示.则下列结论:①
abc >0;②a-b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )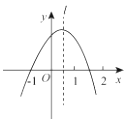
A.①③
B.②③
C.②④
D.②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形 △CBD和△ABC相似,∠A =46°,则 ∠ACB的度数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】教科书中这样写道:“我们把多项式
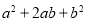 及
及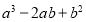 叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.例如:分解因式
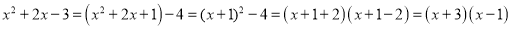 ;例如求代数式
;例如求代数式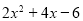 的最小值.
的最小值.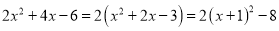 .可知当
.可知当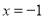 时,
时,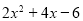 有最小值,最小值是
有最小值,最小值是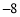 ,根据阅读材料用配方法解决下列问题:
,根据阅读材料用配方法解决下列问题:(1)分解因式:
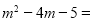 _____
_____(2)当
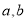 为何值时,多项式
为何值时,多项式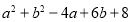 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.(3)当
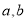 为何值时.多项式
为何值时.多项式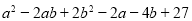 有最小值并求出这个最小值
有最小值并求出这个最小值
相关试题

