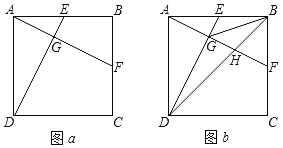
【题目】如图a,在正方形ABCD中,E、F分别为边AB、BC的中点,连接AF、DE交于点G.
(1)求证:AF⊥DE;
(2)如图b,连接BG,BD,BD交AF于点H.
①求证:GB2=GAGD;
②若AB=10,求三角形GBH的面积.
参考答案:
【答案】(1)证明见解析;(2)①证明见解析;②![]()
【解析】
(1)利用正方形性质结合题意得出AE=BF,由此进一步证明△ADE与△BAF全等,从而得出∠BAF=∠ADE,再进一步通过等量代换求得∠ADE+∠DAF=90°,据此进一步分析即可证明结论;
(2)①首先证明△ABN△DAG得出AG=BN,DG=AN,然后再根据EG∥BN得出![]() ,所以AG=GN,最后利用勾股定理可知在Rt△BNG中BG2=BN2+GN2,由此通过等量代换进一步证明结论即可;②首先通过勾股定理求出DE,然后利用三角形等面积法求出AG,从而得知GN与BN,进一步利用△DGH~△BNH得出GH=2HN,然后结合题意计算出GH,最后进一步计算答案即可.
,所以AG=GN,最后利用勾股定理可知在Rt△BNG中BG2=BN2+GN2,由此通过等量代换进一步证明结论即可;②首先通过勾股定理求出DE,然后利用三角形等面积法求出AG,从而得知GN与BN,进一步利用△DGH~△BNH得出GH=2HN,然后结合题意计算出GH,最后进一步计算答案即可.
(1)∵正方形ABCD,E、F分别为边AB、BC的中点,
∴AD=BC=DC=AB,AE=BE=![]() AB,BF=CF=
AB,BF=CF=![]() BC,
BC,
∴AE=BF,
∵在△ADE和△BAF中,
∵
∴△ADE△BAF(SAS)
∴∠BAF=∠ADE,
∵∠BAF+∠DAF=90°,
∴∠ADE+∠DAF=90°,
∴∠AGD=90°,
∴AF⊥DE;
(2)①如图b,过点B作BN⊥AF于N,
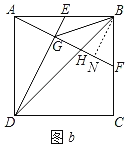
由(1)可得:∠BAF=∠ADE,∠AGD=90°,AB=AD,
∴在△ABN与△DAG中,∠AGD=∠ANB=90°,∠BAF=∠ADE,AB=AD,
∴△ABN△DAG(AAS)
∴AG=BN,DG=AN,
∵∠AGE=∠ANB=90°,
∴EG∥BN,
∴![]() ,且AE=BE,
,且AE=BE,
∴AG=GN,
∴AN=2AG=DG,
∵在Rt△BNG中,BG2=BN2+GN2,
∴BG2=AG2+AG2,
∴GB2=2AG2=2AGAG=GAGD,
即:GB2=GAGD;
②∵AB=10,
∴AE=BF=5,
∴DE=![]() =
=![]() =5
=5![]() ,
,
∵![]() ×AD×AE=
×AD×AE=![]() ×DE×AG,
×DE×AG,
∴AG=2![]() ,
,
∴AG=GN=BN=2![]() ,
,
∴AN=DG=4![]() ,
,
∵GE∥BN,
∴△DGH~△BNH,
∴![]() =
=![]() =2,
=2,
∴GH=2HN,
∵GH+HN=GN=2![]() ,
,
∴GH=![]() ,
,
∴△GBH的面积=![]() ×GH×BN=
×GH×BN=![]() ×
×![]() ×2
×2![]() =
=![]() .
.
-
科目: 来源: 题型:
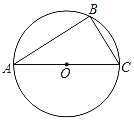
查看答案和解析>>【题目】如图,已知⊙O为△ABC的外接圆,AC为直径,且AC=2
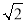 .
.(1)用尺规作图作出∠ABE=45°,与弧AC交于E点(保留作图痕迹,不写作法);
(2)若∠A=30°,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育老师统计了七年级甲、乙两个班女生的身高,并绘制了以下不完整的统计图.

请根据图中信息,解决下列问题:
(1)两个班共有女生多少人?
(2)将频数分布直方图补充完整;
(3)求扇形统计图中
 部分所对应的扇形圆心角度数;
部分所对应的扇形圆心角度数;(4)身高在
 的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率. -
科目: 来源: 题型:
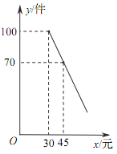
查看答案和解析>>【题目】某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l为y=
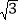 x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).
x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).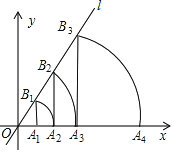
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=145°.其中正确的个数是( )

A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织了一次七年级科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品,C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.
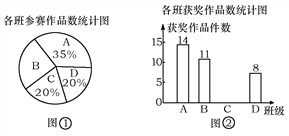
(1)B班参赛作品有多少件?
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
相关试题

