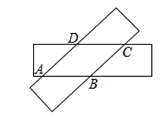
【题目】将两张宽度相等的矩形叠放在一起得到如图所示的四边形ABCD,则四边形ABCD是___________形,若两张矩形纸片的长都是10,宽都是4,那么四边形ABCD周长的最大值=___________.
参考答案:
【答案】菱形; 23.2.
【解析】
易得四边形是平行四边形,再根据宽度相等,利用面积的不同求法可得一组邻边相等,根据一组邻边相等的平行四边形是菱形判断出四边形的形状;
菱形的周长最大,那么边长应最大,即纸条的长度减去菱形的长与菱形长,纸条宽构成直角三角形,求出边长后乘4即为最大周长.
解:如图,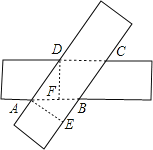
∵AD∥BC,DC∥AB,
∴四边形ABCD是平行四边形.
分别过点A、D作AE⊥BC于E,DF⊥AB于F.
∵两张矩形纸片的宽度相等,
∴AE=DF,
又∵AEBC=DFAB=SABCD,
∴BC=AB,
∴ABCD是菱形;
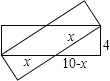
四边形ABCD周长的最大时,
设菱形的边长是x,则x2=(10-x)2+16,解得x=5.8,
所以四边形ABCD周长的最大值=23.2.
故答案为:菱形,23.2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,运算结果正确的是( )
A.(﹣1)3+(﹣3.14)0+2﹣1=﹣
B.2x﹣2=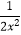
C.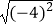 =﹣4
=﹣4
D.a2a3=a5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 且
且 点在线段
点在线段 上,连接
上,连接 .
.(1)如图1,若
 求线段
求线段 的长;
的长;
(2)如图1,若
 求证:
求证:
(3)如图2,在第(2)问的条件下,若点
 在
在 的延长线上时,连接
的延长线上时,连接 的面积为
的面积为 的面积为
的面积为 的面积为
的面积为 .直接写出
.直接写出 之间的数量关系.
之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的面积为6,AC3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的
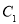 处,P为直线AD上的任意一点,则线段BP的最短长度为_____________.
处,P为直线AD上的任意一点,则线段BP的最短长度为_____________.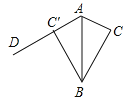
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE∥BC,EF∥AB,则下列结论错误的是( )
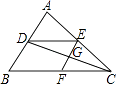
A. =
= 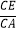
B.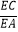 =
= 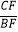
C.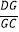 =
= 
D.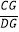 =
= 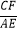
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在如图所示的平面直角坐标系中,依次连接下列各点: A(-5,0),B(1,4),C(3,3),D(1,0),E(3,-3),F(1,-4).

(2)请你在如图所示的方格纸上按照如下要求设计直角三角形:

①使它的三边中有一边边长不是有理数;
②使它的三边中有两边边长不是有理数;
③使它的三边边长都不是有理数.
-
科目: 来源: 题型:
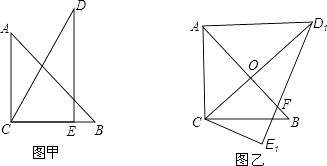
查看答案和解析>>【题目】把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长为( )
A.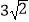
B.5
C.4
D.
相关试题

