【题目】已知△ABC内接于⊙O,AC是⊙O的直径,D是![]() 的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E.
的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E. 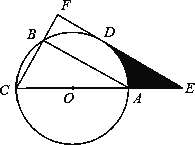
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若CF=6,∠ACB=60°,求阴影部分的面积.
参考答案:
【答案】(1)直线EF与圆O相切(2)8![]() -
-![]()
【解析】试题分析:(1)、首先根据直径所对的圆周角为直角得出∠ABC=∠F=90°,从而得出AB∥EF,根据弧的中点得出OD⊥AB,从而根据平行线得出OD⊥EF,从而得出切线;(2)、首先根据Rt△CEF的勾股定理求出CE、EF和CF的长度,然后根据题意得出△ODE和△CEF相似求出DE的长度,最后根据阴影部分的面积等于△ODE的面积减去扇形OAD的面积求出答案.
试题解析:(1)直线EF与圆O相切,
理由为: 连接OD,如图所示: ∵AC为圆O的直径,∴∠CBA=90°, 又∵∠F=90°,
∴∠CBA=∠F=90°, ∴AB∥EF, ∴∠AMO=∠EDO, 又∵D为![]() 的中点,
的中点,
∴![]() , ∴OD⊥AB, ∴∠AMO=90°, ∴∠EDO=90°, 则EF为圆O的切线;
, ∴OD⊥AB, ∴∠AMO=90°, ∴∠EDO=90°, 则EF为圆O的切线;
(2)在Rt△CEF中,∠ACB=60°,∴∠E=30°, 又∵CF=6, ∴CE=2CF=12,
根据勾股定理得:EF=![]() =6
=6![]() ,
,
在Rt△ODE中,∠E=30°, ∴OD=OE,又OA=OE, ∴OA=AE=OC=CE=4,OE=8,
又∵∠ODE=∠F=90°,∠E=∠E, ∴△ODE∽△CFE, ∴![]() , 即
, 即![]() ,
,
解得:DE=4![]() , 又∵Rt△ODE中,∠E=30°, ∴∠DOE=60°,
, 又∵Rt△ODE中,∠E=30°, ∴∠DOE=60°,
则S阴影=S△ODE-S扇形OAD=×4×4![]() -
-![]() =8
=8![]() -
-![]()
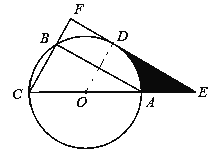
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅游景点的门票价格如下表:
购票人数/人
1﹣50
51﹣100
100以上
每人门票价/元
80
75
70
某校八年级(1)、(2)两班共100多人计划去游览该景点,其中(1)班人数少于50人,(2)班人数有50多人,如果两班都以班为单位单独购票,则一共支付7965元;如果两班联合起来作为一个团体购票,则只需花费7210元.两个班各有多少名学生?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38 ①,然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39 ②,
②一①得:3S―S=39-1,即2S=39-1,
∴S=
 .
.得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)2x﹣1=3
(2)2(3﹣x)=﹣4x+5
(3)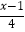 =
= 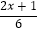 +1.
+1. -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品公司产销一种食品,已知每月的生产成本y1与产量x之间是一次函数关系,函数y1与自变量z(kg)的部分对应值如下表:
x(单位:kg)
10
20
30
y1(单位:/元)
3030
3060
3090
(1)求y1与x之间的函数关系式;
(2)经过试销发现,这种食品每月的销售收入y2(元)与销量x(kg)之间满足如图所示的函数关系
①y2与x之间的函数关系式为;
(3)②假设该公司每月生产的该种食品均能全部售出,那么该公司每月至少要生产该种食品多少kg,才不会亏损? -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)
m﹣( m﹣1)+3(4﹣m),其中m是最大的负整数.
m﹣1)+3(4﹣m),其中m是最大的负整数.
(2)7a2b+(﹣4a2b+5c)﹣2(2a2b+3c),其中ab=1,a+c=5. -
科目: 来源: 题型:
查看答案和解析>>【题目】求证:不论k为何值,关于x的方程 x2+(k+4)x+2k-1=0一定有两个不相等的实数根。
相关试题

